ForceCalculation.h File Reference

Strategy functions for calculating the force effective on one or more particles. More...

#include "objects/CellContainer.h"
#include "objects/ParticleContainer.h"

Go to the source code of this file.

Macros
#define	SQR(x)   ((x) * (x))
#define	SQRT2   1.41421356237309504880
#define	LJTHRESHOLD   1.12246204831

Functions
void	calculateF_Gravity (ParticleContainer &particles, double, CellContainer *lc=nullptr)
	Calculates the force \( F \) for all particles using a naive approach for a Gravity simulation.
void	calculateF_LennardJones (ParticleContainer &particles, double, CellContainer *lc=nullptr)
	Calculates the force \( F \) for all particles using a naive approach for a LennardJones simulation.
void	calculateF_LennardJones_LC (ParticleContainer &particles, double, CellContainer *lc)
	Calculates the force \( F \) for all particles using a naive approach for a linked-cell LennardJones simulation and a cutoff radius.
void	calculateF_LennardJones_LC_task (ParticleContainer &particles, double, CellContainer *lc)
	Calculates the force \( F \) for all particles using a naive approach for a linked-cell LennardJones simulation and a cutoff radius using a task-based parallelization approach.
void	calculateF_Membrane_LC (ParticleContainer &particles, double, CellContainer *lc)
	Calculates the force \( F \) for all particles in a linked-cell membrane simulation using a standard parallelization approach.

Detailed Description

Strategy functions for calculating the force effective on one or more particles.

Date

2024-11-11

Copyright

Copyright (c) 2024

Macro Definition Documentation

LJTHRESHOLD

#define LJTHRESHOLD   1.12246204831

SQR

#define SQR

(

x

)

((x) * (x))

SQRT2

#define SQRT2   1.41421356237309504880

Function Documentation

calculateF_Gravity()

void calculateF_Gravity	(	ParticleContainer &	particles,
		double	,
		CellContainer *	lc = nullptr
	)

Calculates the force \( F \) for all particles using a naive approach for a Gravity simulation.

For each particle in the simulation, the method works by first calculating the effective force

\[ F_{ij} = \frac{m_i m_j}{(|| x_i - x_j ||_2)^3} (x_j - x_i) \]

between each distinct pair of particles \( i \) and \( j \). Afterwards, the effective force for a single particle \( i \) is calculated using the formula

\[ F_i = \sum_{j=1, j \neq i}^p F_{ij} \]

where \( p \) denotes the total number of particles.

This method uses Newton's Third Law

\[ F_{ij} = -F_{ji}. \]

to avoid calculating the force twice.

Parameters

particles	The ParticleContainer containing the Particle objects to iterate over.
lc	Unused. Present to allow calling function without last argument.

calculateF_LennardJones()

void calculateF_LennardJones	(	ParticleContainer &	particles,
		double	,
		CellContainer *	lc = nullptr
	)

Calculates the force \( F \) for all particles using a naive approach for a LennardJones simulation.

For each particle in the simulation, the method works by first calculating the effective force

\[ F_{ij} = -\frac{24 \cdot \epsilon}{\left(\|x_i - x_j\|_2\right)^2} \left( \left( \frac{\sigma}{\|x_i - x_j\|_2} \right)^6 - 2 \left( \frac{\sigma}{\|x_i - x_j\|_2} \right)^{12} \right) (x_i - x_j) \]

between each distinct pair of particles \( i \) and \( j \). Afterwards, the effective force for a single particle \( i \) is calculated using the formula

\[ F_i = \sum_{j=1, j \neq i}^p F_{ij} \]

where \( p \) denotes the total number of particles.

This method uses Newton's Third Law

\[ F_{ij} = -F_{ji}. \]

to avoid calculating the force twice.

Complexity: \( O(N^2) \)

The figure below shows a comparison of all previously implemented LennardJones force calculation functions using a 2D square as input (as per Worksheet 3) with the elapsed time in ms on the y-axis and the number of particles the x-axis. Note that many have been removed to streamline optimization and testing.

A comparison of all LJ force calculation functions.

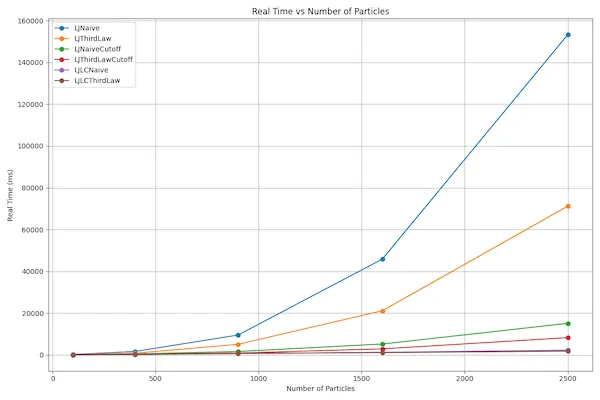
Parameters

particles	The ParticleContainer containing the Particle objects to iterate over.
lc	Unused. Present to allow calling function without last argument.

calculateF_LennardJones_LC()

void calculateF_LennardJones_LC	(	ParticleContainer &	particles,
		double	,
		CellContainer *	lc
	)

Calculates the force \( F \) for all particles using a naive approach for a linked-cell LennardJones simulation and a cutoff radius.

This is an adaptation of the naive Lennard-Jones force calculation, but instead of iterating through every particle pair in the entire container, the algorithm only uses particles within the cell neighborhood of the current particle.

For parallelization, the domain is split into chunks distributed amonst threads. This is done using standard OpenMP loop parallelization.

Complexity: \( O(N) \)

This method uses Newton's Third Law

\[ F_{ij} = -F_{ji}. \]

to avoid calculating the force twice.

The figure below shows the comparison of using the linked cell method with and without applying Newton's third law. The input and the axis descriptions are the same as in the naive algorithm graph.

A comparison of the linked-cell LJ methods.

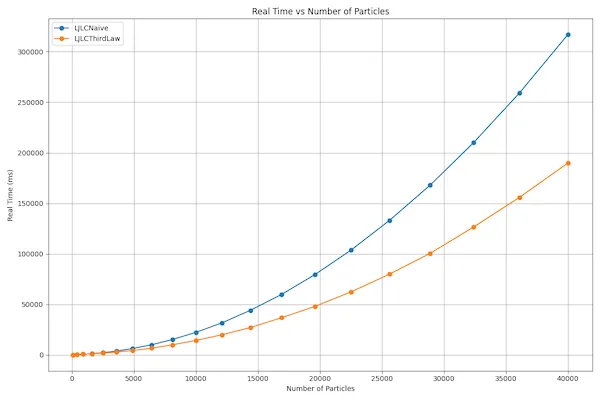
Parameters

particles	The ParticleContainer containing the Particle objects to iterate over.
lc	The CellContainer for the linked cells method.

calculateF_LennardJones_LC_task()

void calculateF_LennardJones_LC_task	(	ParticleContainer &	particles,
		double	,
		CellContainer *	lc
	)

Calculates the force \( F \) for all particles using a naive approach for a linked-cell LennardJones simulation and a cutoff radius using a task-based parallelization approach.

Fundamentally, this is the same algorithm as the base aslgorithm, but instead of splitting chunks of the domain amongst a team of threads, each cell is assigned a separate OpenMP task, distributed among threads via a single delegation thread.

Complexity: \( O(N) \)

This method uses Newton's Third Law

\[ F_{ij} = -F_{ji}. \]

to avoid calculating the force twice.

Parameters

particles	The ParticleContainer containing the Particle objects to iterate over.
lc	The CellContainer for the linked cells method.

calculateF_Membrane_LC()

void calculateF_Membrane_LC	(	ParticleContainer &	particles,
		double	,
		CellContainer *	lc
	)

Calculates the force \( F \) for all particles in a linked-cell membrane simulation using a standard parallelization approach.

For direct particle neighbors inside the membrane, the force is calculated using the formula

\[ F(x_i, x_j) = k \cdot (|| x_i - x_j ||_2 - r_0) \cdot \frac{(x_j - x_i)}{|| x_i - x_j ||_2} \]

between each distinct pair of particles \( i,j \), where \( k \) is the stiffness constant and \( r_0 \) is the average bond length of a molecule pair. For diagonal neighbors, where the average distance is larger, the formula is slightly changed to

\[ F(x_i, x_j) = k \cdot (|| x_i - x_j ||_2 - \sqrt2 r_0) \cdot \frac{(x_j - x_i)}{|| x_i - x_j ||_2}. \]

For certain particles determined during initialization, a special constant upward force along the z-axis \( F_{Z-UP} \) is applied for a set number of iterations. After these iterations, the constant force is no longer applied, and they are treated equally to all other particles.

Complexity: \( O(N) \)

This method uses Newton's Third Law

\[ F_{ij} = -F_{ji}. \]

to avoid calculating the force twice.

Parameters

particles
lc