Grundlagen

• Alphabet \Sigma$\Sigma$: endliche Menge von Symbolen (z.B. \{0,1\}$\{0,1\}$)
• Wort / String über ein Alphabet \Sigma$\Sigma$: endliche Verkettung von Symbolen aus \Sigma$\Sigma$ (z.B. 010$010$)
  • Länge eines Wortes w$w$: |w|$|w|$
  • leere Wort: \epsilon$\epsilon$ (Länge 0)
  • Konkatenation zweier Wörter u$u$ und v$v$: das Wort uv$uv$
    • das leere Wort \epsilon$\epsilon$ konkateniert mit jedem anderen Wort w$w$ ergibt w$w$
    • formal: w^n: \begin{cases}w^0 = \epsilon \\ w^{n+1}=ww^n\end{cases}$w^n: \begin{cases}w^0 = \epsilon \\ w^{n+1}=ww^n\end{cases}$ (z.B. (ab)^3=ababab$(ab)^3=ababab$)
  • Menge aller Wörter über ein Alphabet \Sigma$\Sigma$: \Sigma^*$\Sigma^*$
• (formale) Sprache L$L$: Menge von Wörtern über ein Alphabet
  • formal: L \subseteq \Sigma^*$L \subseteq \Sigma^*$
  • \emptyset$\emptyset$ ist eine Sprache mit 0 Wörtern
  • \{\epsilon\}$\{\epsilon\}$ ist eine Sprache mit einem Wort, dem leeren Wort
  • Bemerkung: \{ab\} \neq ab$\{ab\} \neq ab$ (Sprache vs. Wort)

Operationen auf Sprachen

• Konkatenation: die Menge aller Wörter der Gestalt uv$uv$, wobei u$u$ ein Wort aus der Sprache A$A$ und v$v$ ein Wort aus der Sprache B$B$ ist
  • formal: AB = \{uv \; | \; u \in A \land v \in B \}$AB = \{uv \; | \; u \in A \land v \in B \}$
  • Beispiel: \{ab,b\}\{a,bb\} = \{aba, abbb, ba, bbb\}$\{ab,b\}\{a,bb\} = \{aba, abbb, ba, bbb\}$
• "Selbstkonkatenation", n-malig: die Konkatenation von A$A$ mit sich selbst, n$n$ mal
  • formal: A^n = \{w_1, ..., w_n \; | \; w_1, ..., w_n \in A\} = A...A$A^n = \{w_1, ..., w_n \; | \; w_1, ..., w_n \in A\} = A...A$
    • die Menge mit dem leeren Wort \{\epsilon\}$\{\epsilon\}$ konkateniert mit jeder anderen Sprache A$A$ ergibt A$A$
  • formal, rekursiv: \begin{cases}A^0 = \{\epsilon\} \\ A^{n+1}=AA^n\end{cases}$\begin{cases}A^0 = \{\epsilon\} \\ A^{n+1}=AA^n\end{cases}$
  • Beispiel: \{ab,ba\}^2 = \{ab,ba\}\{ab,ba\} = \{abab, abba, baab, baba\}$\{ab,ba\}^2 = \{ab,ba\}\{ab,ba\} = \{abab, abba, baab, baba\}$
• Kleenesche Hülle: die Menge aller Wörter, die durch beliebige Konkatenation von Wörtern der Sprache A$A$ gebildet werden können (immer inkl. leeres Wort!)
  • formal: A^* = \{w_1, ..., w_n \; | \; n \geq 0 \land w_1, ... , w_n \in A\} = \bigcup_{n\in\N}A^n = A^0 \cup A^1 \cup A^2 \cup ...$A^* = \{w_1, ..., w_n \; | \; n \geq 0 \land w_1, ... , w_n \in A\} = \bigcup_{n\in\N}A^n = A^0 \cup A^1 \cup A^2 \cup ...$
  • (!): \forall A: \epsilon \in A^*$\forall A: \epsilon \in A^*$
  • (!): \emptyset^* = \{\epsilon\}$\emptyset^* = \{\epsilon\}$
  • Beispiel: \{01\}^* = \{\epsilon, 01, 0101, 010101, ...\}$\{01\}^* = \{\epsilon, 01, 0101, 010101, ...\}$
    • Bemerkung: \{01\}^* \neq \{0,1\}^*$\{01\}^* \neq \{0,1\}^*$
• positive Hülle: die Menge aller Wörter, die durch beliebige Konkatenation von Wörtern der Sprache A$A$ gebildet werden können, die nur dann das leere Wort enthalten, wenn das leere Wort selbst Element der Sprache ist
  • formal: A^+ = AA^* = \bigcup_{n\geq1}A^n = A^1 \cup A^2 \cup ...$A^+ = AA^* = \bigcup_{n\geq1}A^n = A^1 \cup A^2 \cup ...$
• (*) kartesisches Produkt: nicht explizit eine Operation auf Sprachen, aber da die Sprachen A, B$A, B$ selber Mengen sind, geht es auch hier
  • Beispiel: \{ab, b\} \times \{a,bb\} = \{(ab,a), (ab,bb), (b,a), (b,bb)\}$\{ab, b\} \times \{a,bb\} = \{(ab,a), (ab,bb), (b,a), (b,bb)\}$

Bonus: Beweisrezepte

• X \subseteq Y$X \subseteq Y$?
  • sei w \in X \implies ... \implies w \in Y$w \in X \implies ... \implies w \in Y$
• irgendwas \implies X \subseteq Y$\implies X \subseteq Y$?
  • Annahme: irgendwas
  • sei w \in X \implies ... \implies$w \in X \implies ... \implies$ (Annahme) ... \implies ... \implies w \in Y$... \implies ... \implies w \in Y$
• X = Y$X = Y$?
  • zeige X \subseteq Y$X \subseteq Y$, dann Y \subseteq X$Y \subseteq X$ getrennt

Rechenregeln für Operationen auf Sprachen

• \emptyset A = \emptyset$\emptyset A = \emptyset$ (die Konkatenation der leeren Menge mit jeder anderen Sprache ist \emptyset$\emptyset$)
• \{\epsilon\}A = A$\{\epsilon\}A = A$ (die Konkatenation einer Sprache, die nur die leere Menge enthält, mit jeder anderen Sprache A$A$ ergibt A$A$)
• A(B\cup C) = AB \cup AC$A(B\cup C) = AB \cup AC$ bzw. (A \cup B) C = AC \cup BC$(A \cup B) C = AC \cup BC$
  • (!) idR gilt A(B \cap C) = AB \cap AC$A(B \cap C) = AB \cap AC$ nicht
• A^* A^* = A^*$A^* A^* = A^*$

Grammatiken

• Grammatik: 4-Tupel G = (V, \Sigma, P, S)$G = (V, \Sigma, P, S)$
  • Vokabular V$V$: endliche Menge von Nichtterminalzeichen (konv. großgeschrieben)
  • Alphabet \Sigma$\Sigma$: endliche Menge von Terminalzeichen (konv. kleingeschrieben), disjunkt von V$V$
  • Produktionsmenge P \subseteq (V \cup \Sigma)^* \times (V \cup \Sigma)^*$P \subseteq (V \cup \Sigma)^* \times (V \cup \Sigma)^*$: endliche Menge von Produktionsregeln
  • Startsymbol S \in V$S \in V$
• Ableitung: der Vorgang, ein Wort nach den Regeln einer formalen Grammatik zu erzeugen
  • formal: \alpha_1 \to_G \alpha_2 \to_G ... \to_G \alpha_n$\alpha_1 \to_G \alpha_2 \to_G ... \to_G \alpha_n$ ("\alpha_n$\alpha_n$ aus \alpha_1$\alpha_1$ gebildet")
  • wenn \alpha_1 = S$\alpha_1 = S$ (die erste Konstruktion das Startsymbol ist) und \alpha_n \in \Sigma^*$\alpha_n \in \Sigma^*$ (die letzte Konstruktion nur aus Terminalzeichen besteht), dann erzeugt die Grammatik G$G$ das Wort \alpha_n$\alpha_n$
  • L(G)$L(G)$: Sprache von G$G$; die Menge aller Wörter, die von G$G$ erzeugt werden
    • formal: L(G) = \{w \in \Sigma^* \; | \; S \to_G^* w\}$L(G) = \{w \in \Sigma^* \; | \; S \to_G^* w\}$ (die Sprache besteht nur aus Terminalzeichen und kann von S$S$ nach n$n$ Schritten erzeugt werden)
    • um zu beweisen, dass eine Grammatik eine Sprache nicht erzeugt, genügt es, ein einziges Gegenbeispiel zu finden (also ein Wort, welches von der Grammatik erzeugt werden kann, aber nicht in der Sprache enthalten ist)
• eine Grammatik G$G$ induziert eine Ableitungsrelation \to_G$\to_G$ auf Wörtern über V \cup \Sigma$V \cup \Sigma$
  • formal: \alpha \to_G \alpha' \iff \beta \to \beta' \in P \land \exists \alpha_1, \alpha_2 : \alpha = \alpha_1 \beta \alpha_2 \land \alpha' = \alpha_1\beta'\alpha_2$\alpha \to_G \alpha' \iff \beta \to \beta' \in P \land \exists \alpha_1, \alpha_2 : \alpha = \alpha_1 \beta \alpha_2 \land \alpha' = \alpha_1\beta'\alpha_2$
    • \alpha \to_G^0 \alpha$\alpha \to_G^0 \alpha$
    • \alpha \to_G^{n+1} \gamma \iff \exists \beta: \alpha \to_G^n \beta \to_G \gamma$\alpha \to_G^{n+1} \gamma \iff \exists \beta: \alpha \to_G^n \beta \to_G \gamma$ (man kann nach n + 1$n + 1$ Schritten von \alpha$\alpha$ ausgehend \gamma$\gamma$ erreichen)
    • \alpha \to_G^* \beta \iff \exists n: \alpha \to_G^n \beta$\alpha \to_G^* \beta \iff \exists n: \alpha \to_G^n \beta$ (\beta$\beta$ ist aus \alpha$\alpha$ erreichbar)
    • \alpha \to_G^+ \beta \iff \exists n > 0: \alpha \to_G^n \beta$\alpha \to_G^+ \beta \iff \exists n > 0: \alpha \to_G^n \beta$ (\beta$\beta$ ist aus \alpha$\alpha$ nach mindestens einem Schritt erreichbar)
  • Beispiel: a + \underline{\lang\text{Term}\rang} + b \to_G a + \underline{\lang\text{Term}\rang \cdot \lang\text{Factor}\rang} + b$a + \underline{\lang\text{Term}\rang} + b \to_G a + \underline{\lang\text{Term}\rang \cdot \lang\text{Factor}\rang} + b$
• (!) Grammatiken mit invaliden Produktionen erzeugen die leere Sprache
  • Beispiel: S \to aS \;|\; bS \implies L(G) = \emptyset$S \to aS \;|\; bS \implies L(G) = \emptyset$

Chomsky-Hierarchie

• Chomsky-Hierarchie: Hierarchie von Klassen formaler Grammatiken, die formale Sprachen erzeugen
  • Typ 0 (Phasenstrukturgrammatik): alle Grammatiken
    • Sprachenklasse: rekursiv aufzählbare Sprachen (Sprachen, die von einer Turingmaschine akzeptiert werden können)
  • Typ 1 (kontextsensitive Grammatik): Typ 0 Grammatiken, wobei jede Produktion länger und länger wird
    • formal: für jede Produktion \alpha \to \beta$\alpha \to \beta$ außer S \to \epsilon$S \to \epsilon$ gilt |\alpha| \leq |\beta|$|\alpha| \leq |\beta|$
    • Sprachklasse: kontextsensitive Sprachen
  • Typ 2 (kontextfreie Grammatik): Typ 1 Grammatiken, wobei die linke Seite nur ein nichtterminales Symbol enthält
    • formal: G$G$ ist vom Typ 1 und für jede Produktion \alpha \to \beta$\alpha \to \beta$ gilt \alpha \in V$\alpha \in V$
    • Sprachklasse: kontextfreie Sprachen
  • Typ 3 (rechtslineare / reguläre Grammatik): Typ 2 Grammatiken, bei denen auf der rechten Seite von Produktionen genau ein Terminalsymbol auftreten darf und maximal ein weiteres Nichtterminalsymbol
    • formal: G$G$ ist vom Typ 2 und für jede Produktion \alpha \to \beta$\alpha \to \beta$ außer S \to \epsilon$S \to \epsilon$ gilt \beta \in \Sigma \cup \Sigma V$\beta \in \Sigma \cup \Sigma V$
      • anders: rechte Seite hat entweder die Form X \to a$X \to a$ oder X \to bY$X \to bY$
    • Sprachklasse: reguläre Sprachen
• (!): L(\text{Typ}_3) \subseteq L(\text{Typ}_2) \subseteq L(\text{Typ}_1) \subseteq L(\text{Typ}_0)$L(\text{Typ}_3) \subseteq L(\text{Typ}_2) \subseteq L(\text{Typ}_1) \subseteq L(\text{Typ}_0)$

DFAs und NFAs

• deterministischer endlicher Automat (DFA): ein endlicher Automat, der unter Eingabe eines Zeichens seines Eingabealphabetes (den möglichen Eingaben) von einem Zustand, in dem er sich befindet, in einen eindeutig bestimmten Folgezustand wechselt
  • formal: Quintupel M = (Q, \Sigma, \delta, q_0, F)$M = (Q, \Sigma, \delta, q_0, F)$ mit...
    • ...einer endlichen Menge von Zuständen Q$Q$
    • ...einem endlichen Eingabealphabet \Sigma$\Sigma$ (Menge erlaubter Eingabesymbole)
    • ...einer totalen Übergangsfunktion \delta: Q \times \Sigma \to Q$\delta: Q \times \Sigma \to Q$ (ordnet jedem Paar bestehend aus einem Zustand q \in Q$q \in Q$ und einem Eingabesymbol a \in \Sigma$a \in \Sigma$ einen Nachfolgezustand p \in Q$p \in Q$ zu)
      • anders: von jedem Zustand aus jedes Symbol kommt genau 1 mal vor!
    • ...einem Startzustand q_0 \in Q$q_0 \in Q$
    • ...einer Menge von Endzuständen (akzeptierenden Zuständen) F \subseteq Q$F \subseteq Q$
  • L(M)$L(M)$: von M$M$ akzeptierte Sprache
    • formal: L(M) := \{w \in \Sigma^* \; | \; \hat\delta (q_0, w) \in F\}$L(M) := \{w \in \Sigma^* \; | \; \hat\delta (q_0, w) \in F\}$
      • \hat\delta : Q \times \Sigma^* \to Q$\hat\delta : Q \times \Sigma^* \to Q$ definiert als \begin{cases}\hat\delta(q, \epsilon) = q \\ \hat\delta(q, aw) = \hat\delta(\delta(q,a),w) \text{ für } a \in \Sigma, w \in \Sigma^*\end{cases}$\begin{cases}\hat\delta(q, \epsilon) = q \\ \hat\delta(q, aw) = \hat\delta(\delta(q,a),w) \text{ für } a \in \Sigma, w \in \Sigma^*\end{cases}$
        • Beispiel: \hat\delta(q_0,aaba) = \delta(\delta(\delta(\delta(q_0,a),a),b),a)$\hat\delta(q_0,aaba) = \delta(\delta(\delta(\delta(q_0,a),a),b),a)$
      • \hat\delta(q,a) = \delta(q,a)$\hat\delta(q,a) = \delta(q,a)$
      • \hat\delta(q,wa) = \delta(\hat\delta(q,w),a)$\hat\delta(q,wa) = \delta(\hat\delta(q,w),a)$
• nichtdeterministischer endlicher Automat (NFA): ein endlicher Automat, bei dem es für den Zustandsübergang mehrere gleichwertige Möglichkeiten gibt
  • formal: Quintupel N = (Q, \Sigma, \delta, q_0, F)$N = (Q, \Sigma, \delta, q_0, F)$ mit...
    • ...Q, \Sigma, q_0, F$Q, \Sigma, q_0, F$ wie bei einem DFA
    • ...einer Übergangsfunktion \delta : Q \times \Sigma \to \mathcal{P}(Q)$\delta : Q \times \Sigma \to \mathcal{P}(Q)$ mit \mathcal{P}(Q)$\mathcal{P}(Q)$ die Menge aller Teilmengen von Q$Q$
      • \overline\delta(S,a) := \bigcup_{q \in S}\delta(q,a)$\overline\delta(S,a) := \bigcup_{q \in S}\delta(q,a)$
      • \hat{\overline\delta}: \mathcal{P}(Q) \times \Sigma^* \to \mathcal{P}(Q)$\hat{\overline\delta}: \mathcal{P}(Q) \times \Sigma^* \to \mathcal{P}(Q)$ (die Menge aller Zustände, die sich von einem Zustand in S$S$ aus mit w$w$ erreichen lassen)
  • L(N)$L(N)$: von N$N$ akzeptierte Sprache
    • formal: L(N) := \{w \in \Sigma^* | \hat{\overline\delta}(\{q_0\}, w) \cap F \neq 0\}$L(N) := \{w \in \Sigma^* | \hat{\overline\delta}(\{q_0\}, w) \cap F \neq 0\}$
    • anders: ein NFA akzeptiert ein Wort, wenn es irgendein Pfad zu einem Endzustand gibt
  • NFA mit \epsilon$\epsilon$-Übergängen: NFA mit speziellem Symbol \epsilon \notin \Sigma$\epsilon \notin \Sigma$ und \delta : Q \times ( \Sigma \cup \{ \epsilon \}) \to \mathcal{P}(Q)$\delta : Q \times ( \Sigma \cup \{ \epsilon \}) \to \mathcal{P}(Q)$
    • ein \epsilon$\epsilon$-Übergang kann ausgeführt werden, ohne ein Eingabezeichen zu lesen
    • für jeden \epsilon$\epsilon$-NFA gibt es einen zugehörigen NFA, der die selbe Sprache akzeptiert (3.16)
  • (*) jeder NFA ist ein DFA
• (!) reguläre / erkennbare Sprache: formale Sprache, die u.a. von endlichen Automaten erkannt wird
  • Sprache, die von einem endlichen Automaten akzeptiert wird
  • Sprache, die von einer regulären / rechtslinearen Grammatik (Typ 3) erzeugt wird
  • Sprache, die durch einen regulären Ausdruck dargestellt werden kann
  • Sprache, die endlich viele Residualsprachen hat
• (!) von rechtslinearen Grammatiken zu DFAs:
  • für jede rechtslineare Grammatik G$G$ gibt es einen DFA M$M$ mit L(M) = L(G)$L(M) = L(G)$
  • für jeden DFA M$M$ gibt es eine rechtslineare Grammatik G$G$ mit L(G) = L(M)$L(G) = L(M)$
• (!) Zwischenschritt NFAs...:
  • für jede rechtslineare Grammatik G$G$ gibt es einen NFA N$N$ mit L(N) = L(G)$L(N) = L(G)$
    • Slide 40, 3.9: erstelle für jedes Nichtterminalzeichen einen Zustand und verbinde diese entsp. den Produktionen; erstelle besonderen Endzustand für Terminalzeichen; wandle Zustände in Endzustände um für \epsilon$\epsilon$-Produktionen
  • für jeden NFA N$N$ gibt es einen DFA M$M$ mit L(M) = L(N)$L(M) = L(N)$
    • Slide 43, 3.10: Potenzmengenkonstruktion
  • für jeden DFA M$M$ gibt es eine rechtslineare Grammatik G$G$ mit L(G) = L(M)$L(G) = L(M)$
• (!) alle Automatentypen erkennen die Sprachen der Grammatiken mit Produktionen der Art:
  • X \to aY$X \to aY$
  • X \to a$X \to a$
  • X \to Y$X \to Y$
  • X \to \epsilon$X \to \epsilon$
  • anders: \epsilon$\epsilon$-NFAs, NFAs und DFAs (und RegEx) sind gleichmächtig

Reguläre Ausdrücke

• regulärer Ausdruck (RegEx): eine Zeichenkette, die der Beschreibung von Mengen von Zeichenketten mit Hilfe bestimmter syntaktischer Regeln dient
  • alternative Notation für die Definition von formalen Sprachen
  • \emptyset, \epsilon$\emptyset, \epsilon$ sind reguläre Ausdrücke
  • für jedes Zeichen a$a$ der Zeichenmenge \Sigma$\Sigma$ ist a$a$ ein regulärer Ausdruck
  • sind x,y$x,y$ reguläre Ausdrücke, dann auch...
    • Alternative: (x | y)$(x | y)$ oder (x + y)$(x + y)$
    • Verkettung: (xy)$(xy)$ oder (x \cdot y)$(x \cdot y)$
    • Kleene-Stern: (x^*)$(x^*)$
  • Bindungsstärke: ^* > \cdot > |$^* > \cdot > |$
• Sprachen der regulären Ausdrücke:
  • L(\emptyset) = \emptyset$L(\emptyset) = \emptyset$ (Symbol für leere Menge spezifiziert leere Sprache)
  • L(\epsilon) = \{ \epsilon \}$L(\epsilon) = \{ \epsilon \}$
  • L(a) = \{a\}$L(a) = \{a\}$
  • L(xy) = L(x)L(y) = \{\alpha \beta \; | \; \alpha \in L(x) \land \beta \in L(y)\}$L(xy) = L(x)L(y) = \{\alpha \beta \; | \; \alpha \in L(x) \land \beta \in L(y)\}$
  • L(x|y) = L(x) \cup L(y)$L(x|y) = L(x) \cup L(y)$
  • L(x^*) = L(x)^* = \{\alpha_1...\alpha_n \; | \; n \in \N_0, \alpha_1,...\alpha_n \in L(x)\}$L(x^*) = L(x)^* = \{\alpha_1...\alpha_n \; | \; n \in \N_0, \alpha_1,...\alpha_n \in L(x)\}$
• Ardens Lemma: sind \alpha, \beta, X$\alpha, \beta, X$ reguläre Ausdrücke mit \epsilon \notin L(\alpha)$\epsilon \notin L(\alpha)$, so gilt X \equiv \alpha X | \beta \implies X \equiv \alpha^* \beta$X \equiv \alpha X | \beta \implies X \equiv \alpha^* \beta$
• Äquivalenz: zwei RegEx sind äquivalent gdw. sie die gleiche Sprache darstellen
  • \alpha \equiv \beta \iff L(\alpha) = L(\beta)$\alpha \equiv \beta \iff L(\alpha) = L(\beta)$

Rechenregeln und Abschlusseigenschaften für RegEx

• Rechenregeln für reguläre Ausdrücke:
  • Null und Eins:
    • \emptyset | \alpha \equiv \alpha | \emptyset \equiv \alpha$\emptyset | \alpha \equiv \alpha | \emptyset \equiv \alpha$
    • \emptyset \alpha \equiv \alpha \emptyset \equiv \emptyset$\emptyset \alpha \equiv \alpha \emptyset \equiv \emptyset$
    • \epsilon \alpha \equiv \alpha \epsilon \equiv \alpha$\epsilon \alpha \equiv \alpha \epsilon \equiv \alpha$
    • \emptyset^* \equiv \epsilon$\emptyset^* \equiv \epsilon$
    • \epsilon^* \equiv \epsilon$\epsilon^* \equiv \epsilon$
  • Assoziativität:
    • (\alpha | \beta) | \gamma \equiv \alpha | (\beta | \gamma)$(\alpha | \beta) | \gamma \equiv \alpha | (\beta | \gamma)$
    • (\alpha \beta) \gamma \equiv \alpha (\beta \gamma)$(\alpha \beta) \gamma \equiv \alpha (\beta \gamma)$
  • Kommutativität:
    • \alpha | \beta \equiv \beta | \alpha$\alpha | \beta \equiv \beta | \alpha$
  • Distributivität:
    • \alpha(\beta | \gamma) \equiv \alpha \beta | \alpha \gamma$\alpha(\beta | \gamma) \equiv \alpha \beta | \alpha \gamma$
    • (\alpha | \beta) \gamma \equiv \alpha \gamma | \beta \gamma$(\alpha | \beta) \gamma \equiv \alpha \gamma | \beta \gamma$
  • Idempotenz:
    • \alpha | \alpha \equiv \alpha$\alpha | \alpha \equiv \alpha$
  • Stern:
    • \epsilon | \alpha \alpha^* \equiv \alpha^*$\epsilon | \alpha \alpha^* \equiv \alpha^*$
    • \alpha^* \alpha \equiv \alpha \alpha^*$\alpha^* \alpha \equiv \alpha \alpha^*$
    • (\alpha^*)^* \equiv \alpha^*$(\alpha^*)^* \equiv \alpha^*$
• Abschlusseigenschaften regulärer Sprachen: sind R, R_1, R_2 \subseteq \Sigma^*$R, R_1, R_2 \subseteq \Sigma^*$ reguläre Sprachen, dann auch:
  • R_1R_2$R_1R_2$ (\alpha_1 \alpha_2$\alpha_1 \alpha_2$)
  • R_1 \cup R_2$R_1 \cup R_2$ (\alpha_1 \; | \; \alpha_2$\alpha_1 \; | \; \alpha_2$)
  • R^*$R^*$ (\alpha^*$\alpha^*$)
  • \overline R = \Sigma^* \backslash R$\overline R = \Sigma^* \backslash R$ (DFA: tausche End- und Nichtendzustände)
  • R_1 \cap R_2$R_1 \cap R_2$ (= \overline{\overline{R_1} \cup \overline{R_2}}$= \overline{\overline{R_1} \cup \overline{R_2}}$)
  • R_1 \backslash R_2$R_1 \backslash R_2$ (= R_1 \cap \overline{R_2}$= R_1 \cap \overline{R_2}$)
  • (!) \Sigma^*$\Sigma^*$ ist stets regulär
• Produkt-Automat: DFA, der L(M_1) \cap L(M_2)$L(M_1) \cap L(M_2)$ akzeptiert, mit gemeinsamen Zuständen und Übergängen
  • gegeben: M_1 = (Q_1, \Sigma, \delta_1, s_1, F_1)$M_1 = (Q_1, \Sigma, \delta_1, s_1, F_1)$, M_2 = (Q_2, \Sigma, \delta_2, s_2, F_2)$M_2 = (Q_2, \Sigma, \delta_2, s_2, F_2)$
  • dann: M = (Q_1 \times Q_2, \Sigma, \delta, (s_1, s_2), F_1 \times F_2)$M = (Q_1 \times Q_2, \Sigma, \delta, (s_1, s_2), F_1 \times F_2)$ mit \delta((q_1, q_2), a) = (\delta_1(q_1, a), \delta_2(q_2, a))$\delta((q_1, q_2), a) = (\delta_1(q_1, a), \delta_2(q_2, a))$

Pumping-Lemma (reg. Sprachen)

• Idee: Wörter ab einer gewissen Länge einer Sprache L$L$ kann man irgendwo in der Mitte aufpumpen, so dass man immer noch ein Wort in der Sprache L$L$ erhält
• Pumping-Lemma für reguläre Sprachen (zeige, dass eine Sprache nicht regulär ist; hinreichend): sei R \subseteq \Sigma^*$R \subseteq \Sigma^*$ regulär; dann gibt es ein n > 0$n > 0$, so dass sich jedes z \in R$z \in R$ mit |z| \geq n$|z| \geq n$ so in z = uvw$z = uvw$ zerlegen lässt, dass:
  • v \neq \epsilon$v \neq \epsilon$ (das Wort v$v$ ist nicht leer)
  • |uv| \leq n$|uv| \leq n$ (die beiden Wörter u$u$ und v$v$ haben zusammen höchstens die Länge n$n$)
  • \forall i \geq 0: uv^iw \in R$\forall i \geq 0: uv^iw \in R$ (für jede natürliche Zahl i$i$ ist das Wort uv^iw$uv^iw$ in der Sprache R$R$, also uw, uvw, uvvw, uvvvw...$uw, uvw, uvvw, uvvvw...$)
• Pumping-Zahl: das kleinste n$n$, das die Eigenschaften des Pumping-Lemmas erfüllt
• Tipps:
  • Wort wählen, das fast nicht mehr in der Sprache ist (z.B. wenn man vorne einen kleinen Teil auf- oder abpumpt, ist das neue Wort nicht mehr in der Sprache)
  • Wort wählen, bei dem die ersten n$n$ Symbole gleich sind (leichtere Zerlegung, vermeidet evtl. Fallunterscheidung)
  • skizzieren...
  • gibt es größere Lücken in der Sprache? \to$\to$ wenn ja, wähle Wort welches, wenn aufgepumpt, zwischen einem Wort und dem nächsten in der Sprache liegt
  • oft i=0$i=0$ (wenig abpumpen) bzw. i = 2$i = 2$ (wenig aufpumpen)
• (!) endliche Automaten können nicht unbegrenzt zählen

Entscheidungsverfahren

• Wortproblem: gegeben w$w$ (Wort) und D$D$ (RegEx, DFA, NFA...), gilt w \in L(D)$w \in L(D)$?
  • DFA M$M$: entscheidbar in O(|w|+|M|)$O(|w|+|M|)$
  • NFA N$N$: entscheidbar in O(|Q|^2|w|+|N|)$O(|Q|^2|w|+|N|)$
• Leerheitsproblem: gegeben D$D$, gilt L(D) = \emptyset$L(D) = \emptyset$?
  • DFA: entscheidbar in O(|Q||\Sigma|)$O(|Q||\Sigma|)$
  • NFA: entscheidbar in O(|Q|^2|\Sigma|)$O(|Q|^2|\Sigma|)$
• Endlichkeitsproblem: gegeben D$D$, ist L(D)$L(D)$ endlich?
  • DFA, NFA: entscheidbar
• Äquivalenzproblem: gegeben D_1, D_2$D_1, D_2$, gilt L(D_1) = L(D_2)$L(D_1) = L(D_2)$?
  • DFA: entscheidbar in O(|Q_1||Q_2||\Sigma|)$O(|Q_1||Q_2||\Sigma|)$
  • NFA: entscheidbar in O(2^{|Q_1|+|Q_2|})$O(2^{|Q_1|+|Q_2|})$ bei fixem \Sigma$\Sigma$
  • RegEx: entscheidbar
• die Kodierung der Eingabe (DFA vs. NFA vs. RE) kann entscheidend für die Komplexität eines Problems sein

Minimierung eines DFAs, Äquivalenz von Wörtern

• jede reguläre Sprache hat einen einzigen minimalen Recognizer
  • anders: der (kanonische) Minimalautomat ist eindeutig
• Unterscheidbarkeit: Zustände p$p$ und q$q$ sind unterscheidbar, wenn es ein w \in \Sigma^*$w \in \Sigma^*$ gibt mit \delta(p,w) \in F$\delta(p,w) \in F$ und \delta(q,w) \notin F$\delta(q,w) \notin F$ oder umgekehrt
  • Unterscheidbarkeit pflanzt sich rückwärts fort
• Äquivalenz von Zuständen: Zustände p$p$ und q$q$ sind äquivalent, wenn sie nicht unterscheidbar sind (i.e. für alle w \in \Sigma^*$w \in \Sigma^*$ gilt \delta(p,w) \in F \iff \delta(q,w) \in F$\delta(p,w) \in F \iff \delta(q,w) \in F$)
  • p \equiv_M q \iff L_M(p) = L_M(q)$p \equiv_M q \iff L_M(p) = L_M(q)$, wobei L_M(q) = \{w \in \Sigma^* \; | \; \delta(q,w) \in F\}$L_M(q) = \{w \in \Sigma^* \; | \; \delta(q,w) \in F\}$
• Quotientenautomat: "Kollabierung" von M$M$ bzgl. \equiv$\equiv$
  • der Quotientenautomat M/\equiv$M/\equiv$ ist ein minimaler DFA für L(M)$L(M)$
• Residualsprache von L$L$ bzgl. w$w$: L^w = \{z \in \Sigma^* \; | \; wz \in L\}$L^w = \{z \in \Sigma^* \; | \; wz \in L\}$
  • L' \subseteq \Sigma^*$L' \subseteq \Sigma^*$ ist Residualsprache von L$L$ wenn es w$w$ gibt mit L' = L^w$L' = L^w$
• Äquivalenz von Wörtern: zwei Wörter sind äquivalent, wenn sie die gleiche Residualsprache haben
  • u \equiv_L v \iff L^u = L^v$u \equiv_L v \iff L^u = L^v$
  • anders: u \equiv_L v \iff \forall w \in \Sigma^*: uw$u \equiv_L v \iff \forall w \in \Sigma^*: uw$ und vw$vw$ beide in L$L$ oder beide nicht in L$L$
• Kanonischer Minimalautomat: M_L = (\mathcal{R}_L, \Sigma, \delta_L, L, F_L)$M_L = (\mathcal{R}_L, \Sigma, \delta_L, L, F_L)$ mit \delta_L(R,a) = R^a$\delta_L(R,a) = R^a$ und F_L = \{R \in \mathcal{R}_L \; | \; \epsilon \in R\}$F_L = \{R \in \mathcal{R}_L \; | \; \epsilon \in R\}$
  • jeder minimale DFA ist isomorph zum kanonischen Minimalautomaten
  • "äquivalente Zustände zusammenfassen" \equiv$\equiv$ wähle irgendein Zustand aus einer Äquivalenzklasse und schaue, in welche Äquivalenzklasse mit einer Kante gegangen wird...
• (!) eine Sprache L$L$ ist genau dann regulär, wenn sie endlich viele Residualsprachen hat

Wichtige (nicht-)reguläre Sprachen

• \emptyset$\emptyset$ regulär \implies \Sigma^*$\implies \Sigma^*$ regulär
• alle endlichen Sprachen L \subseteq \Sigma^*, |L| \in \N$L \subseteq \Sigma^*, |L| \in \N$ sind regulär
• alle kontextfreien Sprachen über einem unären Alphabet sind regulär
• die Sprache \{a^ib^j \; | \; i,j \in \N\}$\{a^ib^j \; | \; i,j \in \N\}$ ist regulär
• die Sprache \{a^ib^i \; | \; i \in \N\}$\{a^ib^i \; | \; i \in \N\}$ ist nicht regulär
• die Sprachen \{a^nb^n \; | \; n \leq ...\}$\{a^nb^n \; | \; n \leq ...\}$ (n$n$ begrenzt) sind regulär
• die Sprache \{0^{m^2} \; | \; m \geq 0\}$\{0^{m^2} \; | \; m \geq 0\}$ ist nicht regulär
• die Sprache der wohlgeklammerten Ausdrücke über dem Alphabet \{(,)\}$\{(,)\}$ ist nicht regulär
• die Sprache der arithmetischen Ausdrücke ist nicht regulär
• BONUS: L_k := \{w \in \{0,1\}^* \; | \; \text{das k-letzte Bit von w ist 1}\}$L_k := \{w \in \{0,1\}^* \; | \; \text{das k-letzte Bit von w ist 1}\}$ \to$\to$ jeder DFA M$M$ mit L(M) = L_k$L(M) = L_k$ hat mindestens 2^k$2^k$ Zustände

Überblick: Konversionen

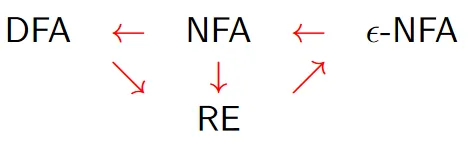
• RE → ϵ-NFA: RE der Länge n$n$ ⇝ O(n)$O(n)$ Zustände
• ϵ-NFA → NFA: Q$Q$ ⇝ Q$Q$
• NFA → DFA: n$n$ Zustände ⇝ O(2^n)$O(2^n)$ Zustände
• NFA → RE: n$n$ Zustände ⇝ RE der Länge O(3^n)$O(3^n)$

Kontextfreie Sprachen, Grammatiken

• linke Seite genau eine Variable, rechte Seite beliebig
• Parsen: Transformation eines Wortes in einen Syntaxbaum (Überprüfung, ob ein Wort von einer Grammatik abgeleitet werden kann)
• kontextfreie Grammatik (CFG): 4-Tupel G = (V,\Sigma,P,S)$G = (V,\Sigma,P,S)$
  • V$V$: endliche Menge von Nichtterminalzeichen (Variablen)
  • \Sigma$\Sigma$: Alphabet von Terminalzeichen (disjunkt von V$V$)
  • P$P$: endliche Menge von Produktionen, P \subseteq V \times (V \cup \Sigma)^*$P \subseteq V \times (V \cup \Sigma)^*$
  • S$S$: Startsymbol, S \in V$S \in V$
• reflexiv transitive Hülle:
  • a \to_G^0 a$a \to_G^0 a$
  • a \to_G^{n+1} \gamma \iff \exists \beta: \alpha \to_G^n \beta \to_G \gamma$a \to_G^{n+1} \gamma \iff \exists \beta: \alpha \to_G^n \beta \to_G \gamma$
  • a \to_G^* \beta \iff \exists n: \alpha \to_G^n \beta$a \to_G^* \beta \iff \exists n: \alpha \to_G^n \beta$
  • a \to_G^+ \beta \iff \exists n > 0: \alpha \to_G^n \beta$a \to_G^+ \beta \iff \exists n > 0: \alpha \to_G^n \beta$
• Linksableitung: Ableitung \alpha_1 \to_G \alpha_2 \to_G ... \to_G \alpha_n$\alpha_1 \to_G \alpha_2 \to_G ... \to_G \alpha_n$, wobei in jedem Schritt das linkeste Nichtterminal in \alpha_i$\alpha_i$ ersetzt wird
• kontextfreie Sprache (CFL): Sprache, die von einer kontextfreien Grammatik erzeugt wird
  • L(G) = \{w \in \Sigma^* \; | \; S \to_G^* w\}$L(G) = \{w \in \Sigma^* \; | \; S \to_G^* w\}$
  • L \in \Sigma^*$L \in \Sigma^*$ kontextfrei \iff G$\iff G$ kontextfrei und L(G)=L$L(G)=L$
• Präfix: u$u$ ist ein Präfix von w$w$, wenn es ein Wort v$v$ gibt, so dass die Konkatenation von u$u$ mit v$v$ das Wort w$w$ ergibt
  • formal: u \preceq w \iff \exists v: uv = w$u \preceq w \iff \exists v: uv = w$
• balancierte Klammerausdrücke: w \in \{[,]\}^*$w \in \{[,]\}^*$ mit A(w) = \#_[(w)m B(w) = \#_](w)$A(w) = \#_[(w)m B(w) = \#_](w)$ ist genau dann balanciert, wenn...
  • A(w) = B(w)$A(w) = B(w)$ (Anz. linke Klammern gleich Anz. rechte Klammern)
  • für alle Präfixe u$u$ von w$w$ gilt A(u) \geq B(u)$A(u) \geq B(u)$
  • intuitiv: addiere 1 bei linke Klammer, subtrahiere 1 bei rechte Klammer; wenn Zahl irgendwann negativ wird oder am Ende nicht 0 ergibt, ist das Wort invalide bzw. die Klammern sind nicht balanciert

Induktionsprinzip

• Induktionsprinzip (S \to \epsilon \; | \; [S] \; | \; SS$S \to \epsilon \; | \; [S] \; | \; SS$): um zu zeigen, dass für alle Wörter u \in L_G(S)$u \in L_G(S)$ eine Eigenschaft P(u)$P(u)$ gilt, zeige...
  • P(\epsilon)$P(\epsilon)$ (Basis; die Eigenschaft gilt für das leere Wort)
  • P(u) \implies P([u])$P(u) \implies P([u])$ (wenn die Eigenschaft für u$u$ gilt, dann auch für [u]$[u]$)
  • P(u) \land P(v) \implies P(uv)$P(u) \land P(v) \implies P(uv)$ (wenn die Eigenschaft für u$u$ und v$v$ gilt, dann auch für uv$uv$)
• (!) Strukturelle Induktion (allgemein): prüfe jede Produktion!
  • für A_i \to w_0 A_{i_1}w_1...w_{n-1}A_{i_n}w_n$A_i \to w_0 A_{i_1}w_1...w_{n-1}A_{i_n}w_n$:
    • Produktion \leftrightarrow$\leftrightarrow$ Erzeugungsregel: u_1 \in L_G(A_{i_1}) \land ... \land u_n \in L_G(A_{i_n}) \implies w_0u_1w_1...u_nw_n \in L_G(A_i)$u_1 \in L_G(A_{i_1}) \land ... \land u_n \in L_G(A_{i_n}) \implies w_0u_1w_1...u_nw_n \in L_G(A_i)$
    • simultane Induktion über die Erzeugung von u$u$: P_{i_1}(u_1) \land ... P_{i_n}(u_n) \implies P_i(w_0u_1w_1...u_nw_n)$P_{i_1}(u_1) \land ... P_{i_n}(u_n) \implies P_i(w_0u_1w_1...u_nw_n)$
  • Beispiel: A \to \epsilon \;|\; aB, B \to Aa$A \to \epsilon \;|\; aB, B \to Aa$
    • \epsilon \in L_G(A)$\epsilon \in L_G(A)$
    • w \in L_G(B) \implies aw \in L_G(A)$w \in L_G(B) \implies aw \in L_G(A)$
    • w \in L_G(A) \implies wa \in L_G(B)$w \in L_G(A) \implies wa \in L_G(B)$
• Produktion: top-down (von Nichtterminal zum Wort)
• Induktion: bottom-up (setze kleinere Wörter zu größeren zusammen)
• w \in L_G(S) \implies P(w)$w \in L_G(S) \implies P(w)$ beweist man immer mit Induktion über Erzeugung von w$w$
• P(w) \implies w \in L_G(S)$P(w) \implies w \in L_G(S)$ beweist man oft mit Induktion über |w|$|w|$

Syntaxbäume

• Syntaxbaum: ein Baum, so dass...
  • jedes Blatt mit einem Zeichen aus \Sigma$\Sigma$ oder \epsilon$\epsilon$ beschriftet ist
  • jeder innere Knoten mit einem Nichtterminalzeichen beschriftet ist
  • ein Blatt \epsilon$\epsilon$ der einzige Nachfolger seines Vorgängers ist
  • von links nach rechts: Produktion
• (!) äquivalente Bedingungen:
  • A \to_G^* w \iff w \in L_G(A) \iff \exists$A \to_G^* w \iff w \in L_G(A) \iff \exists$ Syntaxbaum mit Wurzel A$A$, dessen Blätter von links nach rechts gelesen w$w$ ist
• mehrdeutig: eine CFG heißt mehrdeutig, wenn es ein Wort gibt, das zwei verschiedene Syntaxbäume hat
• inhärent mehrdeutig: eine CFL heißt inhärent mehrdeutig, wenn jede erzeugende CFG mehrdeutig ist (es existiert keine eindeutige Grammatik, die die CFL erzeugt)

Chomsky-Normalform, Greibach-Normalform

• Chomsky-Normalform: jede Produktion hat eine der folgenden Formen...
  • A \to BC$A \to BC$
  • A \to a$A \to a$
  • EXTRA: S \to \epsilon$S \to \epsilon$, dann darf S$S$ nicht auf der rechten Seite einer Produktion stehen!
• Greibach-Normalform: bei jedem Ableitungsschritt entsteht jeweils genau ein Terminalzeichen
  • formal: jede Produktion hat die Form A \to aA_1...A_n$A \to aA_1...A_n$
• (!) zu jeder CFL gibt es eine Grammatik in Chomsky-Normalform (mit L(G') = L(G) \backslash \{\epsilon\}$L(G') = L(G) \backslash \{\epsilon\}$)
• (!) zu jeder CFG gibt es eine Grammatik in Greibach-Normalform (mit L(G') = L(G) \backslash \{\epsilon\}$L(G') = L(G) \backslash \{\epsilon\}$)
• (!) zu jeder CFG kann man eine CFG in Chomsky-Normalform konstruieren (mit L(G') = L(G) \backslash \{\epsilon\}$L(G') = L(G) \backslash \{\epsilon\}$)
• (!) zu jeder CFG kann man eine CFG konstruieren, die keine \epsilon$\epsilon$-Produktionen enthält (mit L(G') = L(G) \backslash \{\epsilon\}$L(G') = L(G) \backslash \{\epsilon\}$)
  • Obermenge \hat P$\hat P$: sind B \to \epsilon$B \to \epsilon$ und A \to \alpha B \beta$A \to \alpha B \beta$ in \hat P$\hat P$, füge auch A \to \alpha \beta$A \to \alpha \beta$ hinzu (rekursiv)
  • definiere neue Grammatik mit Produktionen aus \hat P$\hat P$ ohne \epsilon$\epsilon$-Produktionen (überflüssig)
• Kettenproduktion: A \to B$A \to B$
• (!) zu jeder CFG kann man eine CFG konstruieren, die keine Kettenproduktionen enthält (mit L(G') = L(G)$L(G') = L(G)$)
  • Obermenge \hat P$\hat P$: sind A \to B$A \to B$ und B \to \alpha$B \to \alpha$ in \hat P$\hat P$, füge auch A \to \alpha$A \to \alpha$ hinzu (iterativ)
  • definiere neue Grammatik mit Produktionen aus \hat P$\hat P$ ohne Kettenproduktionen (überflüssig)

Pumping-Lemma (CFL)

• Pumping-Lemma für kontextfreie Sprachen: für jede kontextfreie Sprache L$L$ gibt es ein n \geq 1$n \geq 1$, so dass sich jedes Wort z \in L$z \in L$ mit |z| \geq n$|z| \geq n$ in z = uvwxy$z = uvwxy$ zerlegen lässt mit...
  • vx \neq \epsilon$vx \neq \epsilon$ (mindestens v$v$ oder x$x$ nichtleer)
  • |vwx| \leq n$|vwx| \leq n$
  • \forall i \in \N_0: uv^iwx^iy \in L$\forall i \in \N_0: uv^iwx^iy \in L$

Konstruktion einer Chomsky-Normalform

1. Für jedes Terminalzeichen a$a$, das in einer rechten Seite der Länge \geq 2$\geq 2$ vorkommt
   1.1. Füge ein neues Nichtterminal A_a$A_a$ hinzu
   1.2. Ersetze a$a$ in allen rechten Seiten der Länge \geq 2$\geq 2$ durch A_a$A_a$
   1.3. Füge A_a \to a$A_a \to a$ zu P$P$ hinzu
2. Für jede Produktion der Form A \to B_1B_2...B_k$A \to B_1B_2...B_k$ mit k \geq 3$k \geq 3$
   2.1. Ersetze durch A \to B_1C_2, C_2 \to B_2C_3, ... , C_{k-1} \to B_{k-1}B_k$A \to B_1C_2, C_2 \to B_2C_3, ... , C_{k-1} \to B_{k-1}B_k$ mit C_i$C_i$ neue Nichtterminale
3. Eliminiere alle \epsilon$\epsilon$-Produktionen
4. Eliminiere alle Kettenproduktionen

Abschlusseigenschaften für CFGs / CFLs

• seien G_1, G_2$G_1, G_2$ CFLs; dann kann man in linearer Zeit weitere CFGs konstruieren...
  • L(G_1) \cup L(G_2)$L(G_1) \cup L(G_2)$
  • L(G_1)L(G_2)$L(G_1)L(G_2)$
  • (L(G_1))^*$(L(G_1))^*$
  • (L(G_1))^R$(L(G_1))^R$
• (!) CFLs sind nicht unter Schnitt oder Komplement abgeschlossen

Algorithmen für CFGs

• ein Symbol X \in V \cup \Sigma$X \in V \cup \Sigma$ ist...
  • nützlich \iff$\iff$ es eine Ableitung S \to_G^* w \in \Sigma^*$S \to_G^* w \in \Sigma^*$ gibt, in der das Symbol X$X$ vorkommt
  • erzeugend \iff$\iff$ es eine Ableitung X \to_G^* w \in \Sigma^*$X \to_G^* w \in \Sigma^*$ gibt
  • erreichbar \iff$\iff$ es eine Ableitung S \to_G^* \alpha X \beta$S \to_G^* \alpha X \beta$ gibt
• (!) nützliche Symbole sind erzeugend und erreichbar (aber nicht immer umgekehrt)
• Herleitung einer Grammatik, die die selbe Sprache erzeugt und nur nützliche Symbole enthält:
  1. Aus G$G$: Eliminiere alle nicht erzeugenden Symbole \to G_1$\to G_1$
  2. Aus G_1$G_1$: Eliminiere alle unerreichbaren Symbole \to G_2$\to G_2$
• (!) CFGs - entscheidbar / berechenbar:
  • die Menge der erzeugenden Symbole einer CFG ist berechenbar \implies$\implies$ für eine CFG G$G$ ist entscheidbar, ob L(G) = \emptyset$L(G) = \emptyset$
  • die Menge der erreichbaren Symbole einer CFG ist berechenbar
  • das Wortproblem ist für CFGs in O(|w|^3)$O(|w|^3)$ entscheidbar \to$\to$ CYK-Algorithmus
    • Idee: entscheide das Wortproblem für CFGs in Chomsky-NF
• (!) CFGs - nicht entscheidbar:
  • Äquivalenz: L(G_1) = L(G_2)$L(G_1) = L(G_2)$
  • Schnittproblem: L(G_1) \cap L(G_2) = \emptyset$L(G_1) \cap L(G_2) = \emptyset$
  • Regularität
  • Mehrdeutigkeit

Wichtige CFLs und CFGs

• die nicht-reguläre Sprache L = \{a^nb^n \; | \; n \in \N\}$L = \{a^nb^n \; | \; n \in \N\}$ ist kontextfrei mit S \to aSb \; | \; \epsilon$S \to aSb \; | \; \epsilon$
• die nicht-reguläre Sprache der Palindrome (w = w^R$w = w^R$) über \{a,b\}$\{a,b\}$ ist kontextfrei mit S \to \epsilon \; | \; a \; | \; b \; | \; aSa \; | \; bSb$S \to \epsilon \; | \; a \; | \; b \; | \; aSa \; | \; bSb$
• die Grammatik S \to \epsilon \; | \; [S] \; | \; SS$S \to \epsilon \; | \; [S] \; | \; SS$ erzeugt genau die Menge der balancierten Wörter
• die Sprache \{a^ib^jc^k \;|\; i = j \lor j = k\}$\{a^ib^jc^k \;|\; i = j \lor j = k\}$ ist inhärent mehrdeutig
• die Sprache \{a^ib^ic^i \;|\; i \in \N\}$\{a^ib^ic^i \;|\; i \in \N\}$ ist nicht kontextfrei
• die Sprache \{ww \;|\; w \in \{a,b\}^*\}$\{ww \;|\; w \in \{a,b\}^*\}$ ist nicht kontextfrei
• die Sprache \{ww^R \;|\; w \in \{0,1\}^*\}$\{ww^R \;|\; w \in \{0,1\}^*\}$ ist nicht deterministisch

Kellerautomaten

• (nichtdeterministischer) Kellerautomat (PDA): M = (Q, \Sigma, \Gamma, q_0, Z_0, \delta, F)$M = (Q, \Sigma, \Gamma, q_0, Z_0, \delta, F)$
  • Q, \Sigma, q_0, F$Q, \Sigma, q_0, F$: wie bei DFAs / NFAs
  • \Gamma$\Gamma$: Kelleralphabet
  • Z_0$Z_0$: unterstes Kellerzeichen
  • \delta : Q \times (\Sigma \cup \{\epsilon\}) \times \Gamma \to \mathcal{P_e}(Q \times \Gamma^*)$\delta : Q \times (\Sigma \cup \{\epsilon\}) \times \Gamma \to \mathcal{P_e}(Q \times \Gamma^*)$
    • (q', \alpha) \in \delta(q,a,Z)$(q', \alpha) \in \delta(q,a,Z)$: wenn sich M$M$ im Zustand q$q$ befindet, das Eingabezeichen a$a$ liest und Z$Z$ das oberste Kellerzeichen ist, so kann er im nächsten Schritt in q'$q'$ übergehen und Z$Z$ mit \alpha$\alpha$ ersetzen
      • POP: \alpha = \epsilon$\alpha = \epsilon$, das oberste Kellerzeichen Z$Z$ wird entfernt
      • PUSH: \alpha = Z'Z$\alpha = Z'Z$, das neue Kellerzeichen Z'$Z'$ wird auf dem existierenden Keller gepusht
      • \epsilon$\epsilon$-Übergang: a = \epsilon$a = \epsilon$, ohne Lesen eines Eingabezeichens
• Konfiguration eines Kellerautomaten: (q,w,\alpha)$(q,w,\alpha)$
  • q \in Q$q \in Q$: momentaner Zustand
  • w \in \Sigma^*$w \in \Sigma^*$: noch zu lesender Teil der Eingabe
  • \alpha \in \Gamma^*$\alpha \in \Gamma^*$: aktueller Kellerinhalt (oberstes Kellerzeichen ganz links)
• (!) eine Konfiguration kann mehrere Nachfolger haben
• binäre Relation \to_M$\to_M$:
  • (q,aw,Z_\alpha) \to_M \begin{cases} (q',w,\beta\alpha) &\text{ falls } (q', \beta) \in \delta(q,a,Z) \\ (q',aw,\beta\alpha) &\text{ falls } (q', \beta) \in \delta(q,\epsilon,Z)\end{cases}$(q,aw,Z_\alpha) \to_M \begin{cases} (q',w,\beta\alpha) &\text{ falls } (q', \beta) \in \delta(q,a,Z) \\ (q',aw,\beta\alpha) &\text{ falls } (q', \beta) \in \delta(q,\epsilon,Z)\end{cases}$
  • (q,w,\alpha) \to_M (q', w', \alpha')$(q,w,\alpha) \to_M (q', w', \alpha')$: wenn sich M$M$ in der Konfiguration (q,w,\alpha)$(q,w,\alpha)$ befindet, kann er in einem Schritt in die Nachfolgerkonfiguration (q',w',\alpha')$(q',w',\alpha')$ übergehen
• Akzeptanz mit Endzustand: (q, w, Z_0) \to_M^* (f,\epsilon,\gamma)$(q, w, Z_0) \to_M^* (f,\epsilon,\gamma)$ für f \in F, \gamma \in \Gamma^*$f \in F, \gamma \in \Gamma^*$ (Eingabewort am Ende überarbeitet, Endzustand erreicht, Kellerzustand beliebig)
  • L_F(M) = \{w \;|\; \exists f \in F, \gamma \in \Gamma^* : (q_0,w,Z_0) \to_M^* (f,\epsilon,\gamma)\}$L_F(M) = \{w \;|\; \exists f \in F, \gamma \in \Gamma^* : (q_0,w,Z_0) \to_M^* (f,\epsilon,\gamma)\}$
• Akzeptanz mit leerem Keller: (q, w, Z_0) \to_M^* (q, \epsilon, \epsilon)$(q, w, Z_0) \to_M^* (q, \epsilon, \epsilon)$ für q \in Q$q \in Q$ (Eingabewort am Ende überarbeitet, Keller leer, finaler Zustand beliebig)
  • L_\epsilon(M) = \{w \;|\; \exists q \in Q : (q_0,w,Z_0) \to_M^* (q, \epsilon, \epsilon)\}$L_\epsilon(M) = \{w \;|\; \exists q \in Q : (q_0,w,Z_0) \to_M^* (q, \epsilon, \epsilon)\}$
• (!) Akzeptanz durch Endzustände und leerem Keller gleichmächtig
  • zu jedem PDA M$M$ kann man in linearer Zeit ein PDA M'$M'$ konstruieren mit L_F(M) = L_\epsilon(M')$L_F(M) = L_\epsilon(M')$ (4.49)
    • (q_0, w, Z_0) \to_M^* (f,\epsilon,\gamma) \iff (q_0', w, Z_0') \to_{M'}^*(q,\epsilon, \epsilon)$(q_0, w, Z_0) \to_M^* (f,\epsilon,\gamma) \iff (q_0', w, Z_0') \to_{M'}^*(q,\epsilon, \epsilon)$
  • zu jedem PDA M$M$ kann man in linearer Zeit ein PDA M'$M'$ konstruieren mit L_\epsilon(M) = L_F(M')$L_\epsilon(M) = L_F(M')$ (4.50)
    • (q_0, w, Z_0) \to_M^* (f,\epsilon,\gamma) \iff (q_0', w, Z_0') \to_{M'}^*(q,\epsilon, \epsilon)$(q_0, w, Z_0) \to_M^* (f,\epsilon,\gamma) \iff (q_0', w, Z_0') \to_{M'}^*(q,\epsilon, \epsilon)$
• (!) PDAs und CFGs sind äquivalent
  • CFG \to$\to$ PDA: zu jeder CFG G$G$ kann man einen PDA M$M$ konstruieren so dass L_\epsilon(M) = L(G)$L_\epsilon(M) = L(G)$ (4.53)
    • A \to_G^* u\gamma$A \to_G^* u\gamma$ mit Linksableitung \iff (q,uv,A) \to_M^* (q,v,\gamma)$\iff (q,uv,A) \to_M^* (q,v,\gamma)$
  • PDA \to$\to$ CFG: zu jedem PDA M$M$ (leerer Keller) kann man eine CFG G$G$ konstruieren mit L(G) = L_\epsilon(M)$L(G) = L_\epsilon(M)$ (4.56)
• (!) eine Sprache ist kontextfrei gdw. sie von einem Kellerautomaten akzeptiert wird
• deterministischer Kellerautomat (DPDA): PDA, wobei für jedem Zustand und jedem obersten Kellerzustand höchstens eine Transition existiert
  • formal: \forall q \in Q, a \in \Sigma, Z \in \Gamma: |\delta(q,a,Z)| + |\delta(q,\epsilon,Z)| \leq 1$\forall q \in Q, a \in \Sigma, Z \in \Gamma: |\delta(q,a,Z)| + |\delta(q,\epsilon,Z)| \leq 1$
• deterministische CFL (DCFL): CFL, die von einem DPDA akzeptiert wird
  • (!) jede reguläre Sprache ist eine DCFL
• Präfixbedingung: eine Sprache enthält keine zwei Wörter, so dass das eine ein echtes Präfix des anderen ist
  • \exists$\exists$ DPDA M : L = L_\epsilon(M) \iff \exists$M : L = L_\epsilon(M) \iff \exists$ DPDA M : L = L_F(M)$M : L = L_F(M)$ und L$L$ erfüllt die Präfixbedingung (für eine Sprache L$L$)
• (!) die Klasse der DCFLs ist unter Komplement abgeschlossen \implies$\implies$ DCFLs sind eine echte Teilklasse der CFLs
• (!) die Klasse der DCFLs ist weder unter Schnitt, noch unter Vereinigung abgeschlossen
• (!) jede DCFL ist nicht inhärent mehrdeutig (wird also von einer nicht-mehrdeutigen Grammatik erzeugt)
• (!) das Wortproblem ist für DCFLs in linearer Zeit entscheidbar
• (!) der Schnitt einer kontextfreien Sprache mit einer regulären Sprache ist kontextfrei

Überblick: Abschlusseigenschaften und Entscheidbarkeit

Abschlusseigenschaften

Entscheidbarkeit (DFA / NFA)

Entscheidbarkeit (DFA / PDA / CFG)

Berechenbarkeit, Entscheidbarkeit

• allgemein: man kann jedes Objekt als String oder Zahl kodieren
• Berechenbarkeit: welche Funktionen, die einen String nehmen und einen String zurückgeben / die eine natürliche Zahl nehmen und eine natürliche Zahl zurückgeben, sind berechenbar?
  • intuitiv berechenbar: es gibt ein Algorithmus, der für eine Eingabe (n_1,...,n_k)$(n_1,...,n_k)$ nach endlich vielen Schritten mit Ergebnis f(n_1,...,n_k)$f(n_1,...,n_k)$ hält, falls f$f$ definiert ist, sonst nicht terminiert
  • hier: f: \N^k \to \N$f: \N^k \to \N$ (Strings können als Zahlen kodiert werden, deshalb hier nur \N$\N$)
• Church-Turing-These: die intuitiv berechenbaren Funktionen sind genau die Funktionen, die eine Turing-Machine berechnen kann
  • (!) Turing-Machinen, WHILE-Programme, Registermachinen, High-Level-Programmiersprachen etc. sind alle gleichmächtig
• Funktionen-Terminologie: eine Funktion f: A \to B$f: A \to B$ ist...
  • total: f(a)$f(a)$ ist für alle a \in A$a \in A$ definiert
  • partiell: f(a)$f(a)$ kann auch undefiniert sein
  • echt partiell: f(a)$f(a)$ ist nicht total

(Über-)Abzählbarkeit

• eine Menge M$M$ ist abzählbar, falls... (alle Def. äquivalent)
  • \exists$\exists$ injektive Funktion M \to \N$M \to \N$
  • \exists$\exists$ Bijektion M \to \{0,...,n\}$M \to \{0,...,n\}$ für ein n \in \N$n \in \N$ oder \exists$\exists$ Bijektion M \to \N$M \to \N$
  • \exists$\exists$ Nummerierung der Elemente von M$M$
• eine Menge M$M$ ist überabzählbar, falls sie nicht abzählbar ist
• (!) \Sigma$\Sigma$ endlich \implies \Sigma^*$\implies \Sigma^*$ abzählbar \implies$\implies$ die Menge der Algorithmen ist abzählbar
• (!) die Menge aller Funktionen \N \to \{0,1\}$\N \to \{0,1\}$ ist überabzählbar (Cantors Diagonalargument...)
• (!) es gibt nicht-berechenbare Funktionen \N \to \{0,1\}$\N \to \{0,1\}$ (abzählbar viele Algorithmen, überabzählbare viele Funktionen in \N \to \{0,1\}$\N \to \{0,1\}$)
  • anders: wenn Algorithmen als endliche Wörter kodiert werden können (vgl. Kodierung von TM), dann gibt es unberechenbare Funktionen \N \to \{0,1\}$\N \to \{0,1\}$

Turingmaschinen

• Turingmaschine (TM): M = (Q,\Sigma,\Gamma,\delta,q_0,\square,F)$M = (Q,\Sigma,\Gamma,\delta,q_0,\square,F)$
  • Q$Q$: endliche Menge von Zuständen
  • \Sigma$\Sigma$: endliche Menge des Eingabealphabets
  • \Gamma$\Gamma$: endliche Menge des Bandalphabets, \Sigma \subset \Gamma$\Sigma \subset \Gamma$
  • \delta : Q \times \Gamma \to Q \times \Gamma \times \{L,R,N\}$\delta : Q \times \Gamma \to Q \times \Gamma \times \{L,R,N\}$: Übergangsfunktion
    • \delta$\delta$ darf partiell sein (i.e. \delta(q,a)$\delta(q,a)$ ist nicht definiert für alle q \in F, a \in \Gamma$q \in F, a \in \Gamma$)
    • L,R,N \equiv$L,R,N \equiv$ left, right, nothing (Bewegung des Pointers der Turingmachine)
    • für NTMs (nichtdeterministische TMs): \delta: Q \times \Gamma \to \mathcal{P}(Q \times \Gamma \times \{L,R,N\})$\delta: Q \times \Gamma \to \mathcal{P}(Q \times \Gamma \times \{L,R,N\})$
    • Bedeutung \delta(q,a) = (q',b,D)$\delta(q,a) = (q',b,D)$: wenn sich M$M$ im Zustand q$q$ befindet und auf dem Band a$a$ liest...
      • geht M$M$ im nächsten Schritt in den Zustand q'$q'$ über...
      • überschreibt a$a$ mit b$b$...
      • bewegt den Schreib- / Lesekopf in der Richtung von D$D$ (left, right, nothing)
  • q_0 \in Q$q_0 \in Q$: Startzustand
  • \square \in \Gamma \backslash \Sigma$\square \in \Gamma \backslash \Sigma$: Leerzeichen
  • F \subseteq Q$F \subseteq Q$: Menge der akzeptierenden Zustände / Endzustände
    • für NTMs: eine NTM hält, wenn es mind. einen Weg zu einem akzeptierenden Zustand gibt (mind. ein Weg, das Wort zu akzeptieren)
      • intuitiv: die NTM rät den richtigen Weg
• Konfiguration einer Turingmaschine: (\alpha,q,\beta) \in \Gamma^* \times Q \times \Gamma^*$(\alpha,q,\beta) \in \Gamma^* \times Q \times \Gamma^*$
  • \alpha$\alpha$: was vorher auf dem Band ist
  • q$q$: aktueller Zustand
  • \beta$\beta$: was nachher auf dem Band kommt (beginnend mit dem Zeichen, worauf der Pointer zeigt)
• Relation \to_M$\to_M$: falls \delta(q,\text{first}(\beta)) = (q', c, D)$\delta(q,\text{first}(\beta)) = (q', c, D)$... (formal)
  • (\alpha, q, \beta) \to_M \begin{cases} (\alpha, q', c \text{ rest}(\beta)) &\text{ falls } D=N \\ (\alpha c, q', \text{ rest}(\beta)) &\text{ falls } D=R \\ (\text{butlast}(\alpha), q', \text{last}(\alpha) \; c \text{ rest}(\beta)) &\text{ falls } D=L \end{cases}$(\alpha, q, \beta) \to_M \begin{cases} (\alpha, q', c \text{ rest}(\beta)) &\text{ falls } D=N \\ (\alpha c, q', \text{ rest}(\beta)) &\text{ falls } D=R \\ (\text{butlast}(\alpha), q', \text{last}(\alpha) \; c \text{ rest}(\beta)) &\text{ falls } D=L \end{cases}$
  • für a \in \Gamma, w \in \Gamma^*$a \in \Gamma, w \in \Gamma^*$:
    • \text{first}(aw)=a, \text{first}(\epsilon)=\square$\text{first}(aw)=a, \text{first}(\epsilon)=\square$
    • \text{rest}(aw)=w, \text{rest}(\epsilon)=\epsilon$\text{rest}(aw)=w, \text{rest}(\epsilon)=\epsilon$
    • \text{last}(wa)=a, \text{last}(\epsilon)=\square$\text{last}(wa)=a, \text{last}(\epsilon)=\square$
    • \text{butlast}(wa)=w, \text{butlast}(\epsilon)=\epsilon$\text{butlast}(wa)=w, \text{butlast}(\epsilon)=\epsilon$
  • M$M$ nichtdeterministisch \implies \delta(q,\text{first}(\beta)) \ni (q', c, D)$\implies \delta(q,\text{first}(\beta)) \ni (q', c, D)$
• von TM akzeptierte Sprachen: die TM erreicht irgendwann einen Endzustand und hält
  • formal: L(M) = \{w \in \Sigma^* \; | \; \exists q \in F, \alpha \in \Gamma^*, \beta \in \Gamma^*: (\epsilon, q_0, w) \to_M^* (\alpha, q, \beta)\}$L(M) = \{w \in \Sigma^* \; | \; \exists q \in F, \alpha \in \Gamma^*, \beta \in \Gamma^*: (\epsilon, q_0, w) \to_M^* (\alpha, q, \beta)\}$
  • (!) TM akzeptieren genau Typ-0-Sprachen (alle, die von Grammatiken erzeugt werden)
• Turing-Berechenbarkeit: eine Funktion heißt Turing-berechenbar gdw. sie von einer TM berechnet werden kann
  • formal (Zahlen): f(n_1,...n_k) = m \iff \exists r \in F : (\epsilon, q_0, \text{bin}(n_1)\#...\#\text{bin}(n_k)) \to_M^* (...\square,r, \text{bin}(m)\square...)$f(n_1,...n_k) = m \iff \exists r \in F : (\epsilon, q_0, \text{bin}(n_1)\#...\#\text{bin}(n_k)) \to_M^* (...\square,r, \text{bin}(m)\square...)$
  • formal (Strings): f(u) = v \iff \exists r \in F: (\epsilon, q_0, u) \to_M^* (...\square,r,v\square...)$f(u) = v \iff \exists r \in F: (\epsilon, q_0, u) \to_M^* (...\square,r,v\square...)$
• Halten einer TM: eine TM hält, wenn...
  • ...sie eine Konfiguration (\alpha, q, a\beta)$(\alpha, q, a\beta)$ erreicht und \delta(q,a)$\delta(q,a)$ nicht definiert ist
  • ...sie eine Konfiguration (\alpha, q, a\beta)$(\alpha, q, a\beta)$ erreicht und \delta(q,a) = \emptyset$\delta(q,a) = \emptyset$ (NTM)
  • ...sie einen Endzustand erreicht \implies$\implies$ die von einer TM berechneten Funktion ist wohldefiniert
• (!) zu jeder NTM N$N$ gibt es eine DTM M$M$ mit L(N) = L(M)$L(N) = L(M)$
• k$k$-Band-Turingmaschine (Mehrband-Turingmaschine): TM mit k$k$ Bänder und k$k$ Köpfe (1 Kopf pro Band)
  • Startkonfiguration: Eingabe nur auf dem ersten Band; alle anderen leer
  • \delta : Q \times \Gamma^k \to Q \times \Gamma^k \times \{L,R,N\}^k$\delta : Q \times \Gamma^k \to Q \times \Gamma^k \times \{L,R,N\}^k$
  • (!) die k$k$ Köpfe sind unabhängig voneinander
  • (!) jede k$k$-Band-TM kann durch eine 1-Band-TM simuliert werden (n$n$ Schritte in M \to O(n^2)$M \to O(n^2)$ Schritte in M'$M'$)

WHILE- und GOTO-Programme

• WHILE-Programme: Programme mit WHILE, IF, ELSE, DO, END, :=, +, -, ;, ≠, Variablen x_1,x_2...$x_1,x_2...$, Konstanten c \in \N$c \in \N$
  • berechnet Funktionen f: \N^k \to \N$f: \N^k \to \N$
  • keine negativen Zahlen \to$\to$ negative Ergebnisse werden auf 0 aufgerundet
  • WHILE-Bedingung immer x_i \neq 0$x_i \neq 0$
  • IF-Bedingung immer x_i = 0$x_i = 0$
  • zu Beginn sind alle Eingaben in x_1,...x_k$x_1,...x_k$ für \N^k$\N^k$, sonst sind alle Variablen 0
  • Rückgabewert liegt in x_0$x_0$
  • mit syntaktischem Zucker geht auch die Addition von Variablen miteinander, Multiplikation, Division, Modulo...
  • (!) eine totale Funktion f: \N^k \to \N$f: \N^k \to \N$ ist WHILE-berechenbar gdw. es ein WHILE-Programm gibt, so dass es für alle Eingaben n_1,...n_k$n_1,...n_k$ in x_1,...,x_k$x_1,...,x_k$ mit f(n_1,...,n_k)$f(n_1,...,n_k)$ in x_0$x_0$ terminiert
  • (!) eine partielle Funktion f: \N^k \to \N$f: \N^k \to \N$ ist WHILE-berechenbar gdw. es ein WHILE-Programm gibt, so dass es sich im definierten Fall wie oben verhält, sonst terminiert es nicht (wenn f(n_1,...n_k)$f(n_1,...n_k)$ für die Eingabe undefiniert ist)
  • (!) jede WHILE-berechenbare Funktion ist auch Turing-berechenbar
  • (!) jedes WHILE-Programm ist zu einem WHILE-Programm mit genau einer WHILE-Schleife äquivalent
• GOTO-Programme: Sequenz von markierten Anweisungen mit GOTO ..., IF ... GOTO ... (diesmal X_i = n$X_i = n$ erlaubt) und HALT
  • (!) jedes GOTO-Programm kann durch ein WHILE-Programm simuliert werden
  • (!) jedes WHILE-Programm kann durch ein GOTO-Programm simuliert werden
• (!) jede TM kann durch ein GOTO-Programm simuliert werden (linker / rechter Bandinhalt und Zustand q$q$ als Zahlen kodiert... 5.27)

Entscheidbarkeit

• Entscheidbarkeit: eine Mengeneigenschaft heißt entscheidbar / rekursiv / rekursiv ableitbar, wenn es ein Algorithmus gibt, der für jedes Element der Menge in endlicher Zeit korrekt beantworten kann, ob es die Eigenschaft hat oder nicht; wenn kein solches Entscheidungsverfahren existiert, nennt man die Eigenschaft unentscheidbar
  • formal: eine Teilmenge einer abzählbaren Menge T \subseteq M$T \subseteq M$ heißt entscheidbar, wenn ihre charakteristische Funktion \chi_T: M \to \{0,1\}$\chi_T: M \to \{0,1\}$ berechenbar ist
    • \chi_T(t) = \begin{cases}1 &\text{ falls } t \in T \\ 0 &\text{ sonst }\end{cases}$\chi_T(t) = \begin{cases}1 &\text{ falls } t \in T \\ 0 &\text{ sonst }\end{cases}$
  • formal, anders: sei L \subseteq \Sigma^*$L \subseteq \Sigma^*$ mit Eingabe w \in \Sigma^* \implies w \in L$w \in \Sigma^* \implies w \in L$?
    • L$L$ entscheidbar \iff$\iff$ \exists$\exists$ DTM M$M$ mit L(M)=L$L(M)=L$, die auf jeder Eingabe terminiert \iff \exists$\iff \exists$ DTM M$M$:
      • \forall w \in L: M$\forall w \in L: M$ terminiert und akzeptiert
      • \forall w \notin L: M$\forall w \notin L: M$ terminiert und verwirft (also w \in \Sigma^* \backslash L$w \in \Sigma^* \backslash L$)
  • formal, nochmal anders: Eigenschaft P(x)$P(x)$ entscheidbar \iff \{x \;|\; P(x)\}$\iff \{x \;|\; P(x)\}$ entscheidbar
  • (!) die entscheidbaren Mengen sind abgeschlossen unter Komplement
    • A$A$ entscheidbar \implies \overline A$\implies \overline A$ entscheidbar
    • A$A$ unentscheidbar \implies \overline A$\implies \overline A$ unentscheidbar
• TM-Kodierungsnotation:
  • M_w$M_w$: Kodierung von M$M$ durch w$w$
  • M[w]$M[w]$: Maschine M$M$ mit Eingabe w$w$
  • M[w]\downarrow$M[w]\downarrow$: M[w]$M[w]$ terminiert / hält
• (!) Kodierungsweise irrelevant; ob jetzt 0en und 1en mit #s oder eine andere Kodierung verwendet wird, ändert nicht die Entscheidbarkeit eines Problems

Wichtige Unentscheidbare Probleme

• spezielles Halteproblem: K = \{w \in \{0,1\}^* \; | \; M_w[w] \downarrow\}$K = \{w \in \{0,1\}^* \; | \; M_w[w] \downarrow\}$ (gegeben ein Wort w$w$, hält M_w$M_w$ bei Eingabe w$w$?)
• allgemeines Halteproblem: H = \{w \# x \; | \; M_w[x] \downarrow\}$H = \{w \# x \; | \; M_w[x] \downarrow\}$ (gegeben w$w$ als Kodierung einer TM und x$x$ als Eingabe der TM, hält M_w$M_w$ bei Eingabe x$x$?)
• Halteproblem auf leerem Band / \epsilon$\epsilon$-Halteproblem: H_0 = \{w \in \{0,1\}^* \; | \; M_w[\epsilon] \downarrow\}$H_0 = \{w \in \{0,1\}^* \; | \; M_w[\epsilon] \downarrow\}$
• Äquivalenzproblem: Eq = \{u\#v \; | \; M_u \text{ berechnet die gleiche Funktion wie } M_v\}$Eq = \{u\#v \; | \; M_u \text{ berechnet die gleiche Funktion wie } M_v\}$
• Leerheitsproblem: \text{Empty} = \{w \in \{0,1\}^* \; | \; L(M_w) \neq \emptyset\}$\text{Empty} = \{w \in \{0,1\}^* \; | \; L(M_w) \neq \emptyset\}$ (ist die Sprache der Turingmaschine (nicht-)leer?)
• Hilberts 10. Problem: ob ein Polynom in n$n$ Variablen mit ganzzahligen Koeffizienten eine ganzzahlige Nullstelle hat
• Postsches Korrespondenzproblem (PCP): siehe unten...
• Unentscheidbare Probleme für CFGs G_1, G_2$G_1, G_2$:
  • L(G_1) \cap L(G_2) = \emptyset$L(G_1) \cap L(G_2) = \emptyset$?
  • |L(G_1) \cap L(G_2)| = \infty$|L(G_1) \cap L(G_2)| = \infty$?
  • L(G_1) \cap L(G_2)$L(G_1) \cap L(G_2)$ kontextfrei?
  • L(G_1) \subseteq L(G_2)$L(G_1) \subseteq L(G_2)$?
  • L(G_1) = L(G_2)$L(G_1) = L(G_2)$?
  • G$G$ mehrdeutig?
  • L(G)$L(G)$ regulär?
  • L(G)$L(G)$ deterministisch?
  • L(G) = L(\alpha)$L(G) = L(\alpha)$ mit \alpha$\alpha$ RegEx?
• (!) nicht alle unentscheidbaren Probleme sind gleich schwer (z.B. H \leq Eq, Eq \nleq H$H \leq Eq, Eq \nleq H$)

Reduktionen

• Reduktion: Methode, bei der ein Problem auf ein anderes zurückgeführt wird
  • formal: eine Menge A \subseteq \Sigma^*$A \subseteq \Sigma^*$ ist reduzierbar auf B \subseteq \Gamma^*$B \subseteq \Gamma^*$ gdw. es eine totale berechenbare Funktion f : \Sigma^* \to \Gamma^*$f : \Sigma^* \to \Gamma^*$ gibt mit \forall w \in \Sigma^*: w \in A \iff f(w) \in B$\forall w \in \Sigma^*: w \in A \iff f(w) \in B$
  • Schreibweise; A \leq B$A \leq B$ (A$A$ reduziert auf B$B$)
    • intuitiv: A$A$ "leichter" als B$B$, deshalb \leq$\leq$; aus einen Algorithmus für B$B$ kann man einen Algorithmus für A$A$ gewinnen
  • intuitiv: Verbindung zwischen zwei Entscheidungsproblemen; gibt es einen Algorithmus für das zweite Problem, so lässt sich über die Reduktion auch das erste lösen
  • Idee: gegeben die Eingabe für das erste Problem, ändere die Eingabe durch eine Konverterfunktion und gebe die veränderte Eingabe der zweiten Funktion \to$\to$ das zweite Problem gibt die korrekte Antwort für das erste Problem anhand der veränderten Eingabe (Ja-Instanzen werden auf Ja-Instanzen abgebildet, Nein-Instanzen werden auf Nein-Instanzen abgebildet)
    • die Reduktion bezieht sich legidlich auf die Konverterfunktion...
  • Checkliste:
    • Beschreibung: wie funktioniert f$f$?
    • Totalität: für jedes Element aus A$A$ berechnet die Funktion ein Ergebnis
    • Berechenbarkeit: die einzelnen Schritte sind berechenbar
    • Korrektheit: w \in A \iff ... \iff w' \in B$w \in A \iff ... \iff w' \in B$
  • Schlussfolgerungen: wenn A \leq B$A \leq B$...
    • B$B$ entscheidbar \implies A$\implies A$ entscheidbar
    • B$B$ semientscheidbar \implies A$\implies A$ semientscheidbar
    • A$A$ unentscheidbar \implies B$\implies B$ unentscheidbar
    • A$A$ (semi-)entscheidbar \implies B$\implies B$ ??? (keine Aussage möglich)
    • B$B$ unentscheidbar \implies A$\implies A$ ??? (keine Aussage möglich)

• Satz von Rice: es ist unmöglich, eine beliebige nicht-triviale Eigenschaft der erzeugten Funktion einer Turing-Maschine / eines Algorithmus algorithmisch zu entscheiden
  • intuitiv: alle Probleme der Art "gegeben eine DTM M$M$, hat L(M)$L(M)$ die Eigenschaft..." sind unentscheidbar
  • Reduktionsschema: gegeben DTM M'$M'$, hat L(M')$L(M')$ die Eigenschaft E$E$?
    • Idee: H \leq L$H \leq L$ oder \overline H \leq L$\overline H \leq L$
    • erfüllt \emptyset$\emptyset$ die Eigenschaft E$E$? (ist \emptyset$\emptyset$ die Ja-Instanz?)
      • ja: \overline H \leq L$\overline H \leq L$
        • gegeben M$M$ und w$w$, konstruiere M'$M'$:
          • führe M$M$ auf w$w$ aus (auf anderem Band, um sicherheitshalber das Eingabewort für M'$M'$ zu merken)
          • falls M$M$ auf w$w$ hält, führe eine DTM aus, die die Eigenschaft nicht erfüllt
          • falls diese akzeptiert, akzeptiere, sonst verwirf
      • nein: H \leq L$H \leq L$
        • gegeben M$M$ und w$w$, konstruiere M'$M'$:
          • führe M$M$ auf w$w$ aus (auf anderem Band)
          • falls M$M$ auf w$w$ hält, führe eine DTM aus, die die Eigenschaft erfüllt
          • falls diese akzeptiert, akzeptiere, sonst verwirf
• semantische Eigenschaft: Eigenschaft einer DTM M$M$, die nur von L(M)$L(M)$ abhängt
  • anders: wenn L(M) = L(M')$L(M) = L(M')$, dann erfüllen entweder beide TM die Eigenschaft oder keine
• triviale Eigenschaft: Eigenschaft, die entweder jede DTM erfüllt oder keine

Semi-Entscheidbarkeit / Rekursive Aufzählbarkeit

• Semi-Entscheidbarkeit: eine Mengeneigenschaft heißt semi-entscheidbar, wenn es ein Algorithmus gibt, der für jedes Element der Menge mit der "JA"-Eigenschaft in endlicher Zeit "JA" zurückgibt, sonst nicht terminiert
  • formal: eine Menge A \subseteq \N$A \subseteq \N$ oder A \subseteq \Sigma^*$A \subseteq \Sigma^*$ heißt semi-entscheidbar gdw. die partielle charakteristische Funktion \chi'_A(x)$\chi'_A(x)$ berechenbar ist
    • \chi'_A(x) = \begin{cases}1 &\text{ falls } x \in A \\ \bot &\text{ sonst (terminiert nicht, undefiniert)}\end{cases}$\chi'_A(x) = \begin{cases}1 &\text{ falls } x \in A \\ \bot &\text{ sonst (terminiert nicht, undefiniert)}\end{cases}$
  • co-semi-entscheidbar: wie semi-entscheidbar, nur für "NEIN"
  • Schlussfolgerungen:
    • A$A$ entscheidbar \iff A, \overline A$\iff A, \overline A$ semi-entscheidbar
    • A \leq B$A \leq B$:
      • B$B$ semi-entscheidbar \implies A$\implies A$ semi-entscheidbar
      • A$A$ nicht semi-entscheidbar \implies B$\implies B$ nicht semi-entscheidbar
      • A$A$ nicht co-semi-entscheidbar \implies B$\implies B$ nicht co-semi-entscheidbar
    • L$L$ co-semi-entscheidbar \iff \overline L$\iff \overline L$ semi-entscheidbar
    • L$L$ semi- und co-semi-entscheidbar \iff L$\iff L$ entscheidbar
    • L$L$ semi-entscheidbar \iff L$\iff L$ Turing-erkennbar
  • (!) das Halteproblem ist semi-entscheidbar
• rekursiv aufzählbar: eine Menge A$A$ heißt rekursiv aufzählbar, wenn es einen Algorithmus gibt, der alle "JA"-Instanzen aufzählt
  • funktionsweise: der Algorithmus bekommt keine Eingabe, darf unendlich lange laufen, muss jede JA-Instanz mindestens einmal ausgeben und darf niemals eine NEIN-Instanz ausgeben
  • formal: A$A$ rekursiv aufzählbar \iff A = \emptyset$\iff A = \emptyset$ oder es gibt eine berechenbare totale Funktion f: \N \to A$f: \N \to A$ so dass A = \{f(0), f(1), f(2),...\}$A = \{f(0), f(1), f(2),...\}$, wobei Elemente doppelt auftreten können f(i) = f(j)$f(i) = f(j)$ und die Reihenfolge beliebig ist
  • (!) A$A$ rekursiv aufzählbar \iff A$\iff A$ semi-entscheidbar
• Äquivalenzen: alles hier ist untereinander äquivalent...
  • A$A$ ist semi-entscheidbar
  • A$A$ ist rekursiv aufzählbar
  • A$A$ ist vom Typ 0
  • A = L(M)$A = L(M)$ für eine TM M$M$ (A$A$ ist die Menge aller Berechnungsergebnisse einer TM)
  • \chi'_A$\chi'_A$ ist berechenbar
  • A$A$ ist Definitionsbereich einer berechenbaren Funktion
  • A$A$ ist Wertebereich einer berechenbaren Funktion

Das Postsche Korrespondenzproblem

• Postsches Korrespondenzproblem (PKP / PCP): gegeben beliebig viele Kopien von "Dominosteinen", wo in der oberen und unteren Hälften ein Wort steht; gibt es eine Folge dieser Steine, so dass das zusammengesetzte Wort oben und das Wort unten gleich sind?
  • formal: gegeben eine endliche Folge (x_1, y_1),...,(x_k,y_k); x_i, y_i \in \Sigma^+$(x_1, y_1),...,(x_k,y_k); x_i, y_i \in \Sigma^+$, gibt es eine Folge von Indizes i_1, ...,i_n \in \{1, ..., k\}, n > 0$i_1, ...,i_n \in \{1, ..., k\}, n > 0$ so dass x_{i_1},...,x_{i_n} = y_{i_1},...,y_{i_n}$x_{i_1},...,x_{i_n} = y_{i_1},...,y_{i_n}$
    • wenn ja \to i_1, ..., i_n$\to i_1, ..., i_n$ Lösung der Instanz (x_1,y_1),...,(x_k,y_k)$(x_1,y_1),...,(x_k,y_k)$ des PCP-Problems
  • (!) PCP ist unentscheidbar und semi-entscheidbar
  • Sinn: "das leichteste untentscheidbare Problem" \to$\to$ wird häufig verwendet, um mittels Reduktion die Untentscheidbarkeit eines anderen Problems zu zeigen
  • modifiziertes PCP / MPCP: wie PCP, aber man muss mit dem ersten Dominostein anfangen
  • (!) MPCP \leq$\leq$ PCP
  • (!) H \leq$H \leq$ MPCP
  • Bemerkungen:
    • PCP entscheidbar falls |\Sigma| = 1$|\Sigma| = 1$
    • PCP entscheidbar falls k \leq 2$k \leq 2$
    • PCP unentscheidbar falls k \geq 5$k \geq 5$

Überblick: Klassen von Funktionen

Komplexitätstheorie

• Komplexitätstheorie: wie schnell kann man ein Problem lösen / mit wie viel Speicherplatz kann ich das Problem lösen?
  • hier: nicht Komplexität des Lösungsalgorithmus (z.B. InsertionSort, MergeSort), sondern des Problems (z.B. Arraysortierung)
  • Beschreibung der Komplexität eines Algorithmus:
    • abhängig von der Länge der Eingabe (n$n$)
    • worst-case
    • O-Notation
• Komplexitätsklasse: Menge von Problemen, die sich alle mit denselben Ressourcen lösen lassen (z.B. in gewisser Zeit / mit gewissem Platz)
  • formal (P): \text{time}_M(w) =$\text{time}_M(w) =$ Anzahl der Schritte, bis die DTM M[w]$M[w]$ hält
    • \text{time}_M(w) \in \N \cup \{\infty\}$\text{time}_M(w) \in \N \cup \{\infty\}$ (# Schritte oder M$M$ hält nicht)
  • formal² (P): \text{TIME}(f(n)) =$\text{TIME}(f(n)) =$ die Klasse der in Zeit f(n)$f(n)$ entscheidbaren Sprachen
    • \text{TIME}(f(n)) = \{A \subseteq \Sigma^* \; | \; \exists \text{ DTM } M : A = L(M) \land \forall w \in \Sigma^* : \text{time}_M(w) \leq f(|w|)\}$\text{TIME}(f(n)) = \{A \subseteq \Sigma^* \; | \; \exists \text{ DTM } M : A = L(M) \land \forall w \in \Sigma^* : \text{time}_M(w) \leq f(|w|)\}$ (die DTM entscheidet die Sprache A$A$ in höchstens f(n)$f(n)$ Schritten)
      • Beispiel: f(n) = n^2 \implies M[w]$f(n) = n^2 \implies M[w]$ hält nach höchstens n^2$n^2$ Schritten
  • formal (NP): \text{ntime}_M(w) = \begin{cases} \text{minimale Anzahl der Schritte bis NTM } M[w] \text{ akzeptiert} &\text{ falls } w \in L(M) \\ 0 &\text{ falls } w \notin L(M)\end{cases}$\text{ntime}_M(w) = \begin{cases} \text{minimale Anzahl der Schritte bis NTM } M[w] \text{ akzeptiert} &\text{ falls } w \in L(M) \\ 0 &\text{ falls } w \notin L(M)\end{cases}$
  • formal² (NP): \text{NTIME}(f(n)) = \{A \subseteq \Sigma^* \; | \; \exists \text{ NTM } M : A = L(M) \land \forall w \in \Sigma^* : \text{ntime}_M(w) \leq f(|w|)\}$\text{NTIME}(f(n)) = \{A \subseteq \Sigma^* \; | \; \exists \text{ NTM } M : A = L(M) \land \forall w \in \Sigma^* : \text{ntime}_M(w) \leq f(|w|)\}$ (die NTM entscheidet die Sprache A$A$ in höchstens f(n)$f(n)$ Schritten)
    • äquivalent (NP): die NTM M[w]$M[w]$ muss nach maximal p(|w|)$p(|w|)$ Schritten halten

Komplexitätsklassen P und NP

• Komplexitätsklasse P: Probleme, die von einer DTM in polynomieller Zeit lösbar sind ("effizient lösbare" Probleme)
  • formal: P = \bigcup_{k \geq 0} \text{TIME}(O(n^k))$P = \bigcup_{k \geq 0} \text{TIME}(O(n^k))$
  • anders: P = \{ L \; | \;$P = \{ L \; | \;$es gibt ein Polynom p(n)$p(n)$ und eine p(n)$p(n)$-zeitbeschränkte DTM M$M$ mit L = L(M)\}$L = L(M)\}$
  • Bemerkungen:
    • O(n \log n) \subset O(n^2)$O(n \log n) \subset O(n^2)$
    • \forall k : n^{\log n}, 2^n \notin O(n^k)$\forall k : n^{\log n}, 2^n \notin O(n^k)$
    • A \notin P$A \notin P$ schwierig...
• Komplexitätsklasse NP: Probleme, die von einer NTM in polynomieller Zeit lösbar sind ("effizient verifizierbare" Probleme)
  • formal: NP = \bigcup_{p \text{ Polynom }} \text{NTIME}(p(n))$NP = \bigcup_{p \text{ Polynom }} \text{NTIME}(p(n))$
  • anders: NP = \{ L \; | \;$NP = \{ L \; | \;$es gibt ein Polynom p(n)$p(n)$ und eine p(n)$p(n)$-zeitbeschränkte NTM M$M$ mit L = L(M)\}$L = L(M)\}$
  • Bemerkungen:
    • P \in NP$P \in NP$ (ob P = NP$P = NP$ ist noch offen...)
    • A \in P \implies \overline A \in P$A \in P \implies \overline A \in P$ (tausche End- und Nichtendzustände der TM; gilt nicht für NP)
• NP-Zertifikate: gültige "Lösungsvorschläge" für ein Problem in NP, was leicht (deterministisch, polynomiell) verifizierbar ist
  • formal: DTM M$M$ mit L(M) \subseteq \{w \# c \; | \; w \in \Sigma^*, c \in \Delta^*\}$L(M) \subseteq \{w \# c \; | \; w \in \Sigma^*, c \in \Delta^*\}$
  • anders: M$M$ heißt Verifikator für A$A$ wenn A = \{w \in \Sigma^* \; | \; \exists c \in \Delta^*: w\#c \in L(M)\}$A = \{w \in \Sigma^* \; | \; \exists c \in \Delta^*: w\#c \in L(M)\}$
    • w\#c \in L(M) \implies c$w\#c \in L(M) \implies c$ Zertifikat für w$w$ (w$w$ Eingabe und c$c$ Zertifikat für JA-Instanz)
      • Beispiel (SAT): w$w$ Formel, c$c$ Belegung
      • Beispiel (HAMILTON): w$w$ Graph, c$c$ Pfad
    • |c| \leq p(|w|)$|c| \leq p(|w|)$ (Länge des Zertifikats beschränkt)
  • polynomiell beschränkter Verifikator: M$M$ Verifikator für A$A$ und \exists$\exists$ Polynom p: \text{time}_M(w\#c) \leq p(|w|)$p: \text{time}_M(w\#c) \leq p(|w|)$
  • intuitiv: für ein Problem ist es...
    • schwer zu entscheiden, ob es lösbar ist
    • leicht zu entscheiden, ob ein Lösungsvorschlag eine Lösung (Zertifikat) ist
  • (!) A \in NP \iff \exists$A \in NP \iff \exists$ polynomiell beschränkter Verifikator für A$A$
• allgemein:
  • P$P$: Sprachen, bei denen w \in L$w \in L$ schnell entschieden werden kann
  • NP$NP$: Sprachen, bei denen ein Zertifikat für w \in L$w \in L$ schnell verifiziert werden kann

Wichtige Probleme in P

• \{ww^R \; | \; w \in \Sigma^*\} \in \text{TIME}(O(n^2)) \subseteq P$\{ww^R \; | \; w \in \Sigma^*\} \in \text{TIME}(O(n^2)) \subseteq P$
• \{(G,w) \; | \; G \text{ ist CFG } \land w \in L(G)\} \in P$\{(G,w) \; | \; G \text{ ist CFG } \land w \in L(G)\} \in P$
• \{(G,w) \; | \; G \text{ ist Graph } \land w \text{ ist Pfad in } G\} \in P$\{(G,w) \; | \; G \text{ ist Graph } \land w \text{ ist Pfad in } G\} \in P$
• \{G \; | \; G \text{ hat Eulerkreis}\} \in P$\{G \; | \; G \text{ hat Eulerkreis}\} \in P$ (G$G$ zusammenhängend und jeder Knoten hat geraden Grad)
• \{\text{bin}(p) \; | \; p \text{ ist Primzahl}\} \in P$\{\text{bin}(p) \; | \; p \text{ ist Primzahl}\} \in P$
• 1KNF-SAT \in P$\in P$
• 2KNF-SAT \in P$\in P$

Polyzeitreduktion, NP-Vollständigkeit

• Polyzeitreduktion (polynomiell reduzierbar): Reduktion, wobei f$f$ in Polyzeit berechnet werden kann
  • formal: eine Menge A \subseteq \Sigma^*$A \subseteq \Sigma^*$ ist polynomiell reduzierbar auf B \subseteq \Gamma^*$B \subseteq \Gamma^*$ gdw. es eine totale, von einer DTM in polynomieller Zeit berechenbare Funktion f : \Sigma^* \to \Gamma^*$f : \Sigma^* \to \Gamma^*$ gibt mit \forall w \in \Sigma^*: w \in A \iff f(w) \in B$\forall w \in \Sigma^*: w \in A \iff f(w) \in B$
    • Schreibweise; A \leq_p B$A \leq_p B$ (A$A$ reduziert auf B$B$)
    • Transitivität: \leq_p$\leq_p$ ist transitiv
  • Abgeschlossenheit: P$P$ und NP$NP$ sind unter polynomieller Reduzierbarkeit nach unten abgeschlossen
    • A \leq_p B, B \in P \implies A \in P$A \leq_p B, B \in P \implies A \in P$
    • A \leq_p B, B \in NP \implies A \in NP$A \leq_p B, B \in NP \implies A \in NP$
  • (!) jedes Problem aus P$P$ kann auf jedes andere Problem aus P$P$ reduziert werden
    • Idee: wenn man ein Problem A \in P$A \in P$ auf ein anderes Problem B \in P$B \in P$ reduzieren möchte, kann man eine Funktion angeben, die einfach A$A$ löst (by default in polynomieller Zeit!) und dann ein entsprechendes Beispiel für B$B$ ausgibt
      • Beispiel (Erreichbarkeit in gerichteten Graphen \leq_p$\leq_p$ Nicht-Leerheit eines NFAs):
        • ist t$t$ von s$s$ erreichbar, gebe z.B. NFA nur mit Endzustand zurück (akz. leeres Wort)
        • ist t$t$ von s$s$ erreichbar, gebe z.B. NFA ohne Endzustand zurück (leere Sprache)
• NP-Schwere / NP-Härte: Eigenschaft eines Problems, mindestens so schwer lösbar zu sein wie die Probleme der Klasse NP
  • formal: L$L$ NP-hart \iff \forall A \in NP: A \leq_p L$\iff \forall A \in NP: A \leq_p L$ (alle A$A$ aus NP$NP$ sind polynomiell reduzierbar auf L$L$)
  • können auch außerhalb von NP$NP$ sein...
• NP-Vollständigkeit: Eigenschaft eines Problems in NP, dass man alle anderen Probleme in NP auf dieses Problem reduzieren kann (die "schwierigsten" Probleme der Klasse NP)
  • formal: L$L$ NP-vollständig \iff L$\iff L$ NP-hart und L \in NP$L \in NP$
  • (!) jedes Problem in P$P$ kann auf jedes NP-vollständige Problem reduziert werden
  • (!) jedes NP-vollständige Problem kann auf jedes andere NP-vollständige Problem reduziert werden
  • Idee: P = NP \iff$P = NP \iff$ es wird gezeigt, dass irgendein NP-vollständiges Problem in P$P$ liegt
  • Vermutung: P \neq NP \iff$P \neq NP \iff$ kein NP-vollständiges Problem ist in P

Wichtige NP-vollständige Probleme

• SAT
  • gegeben eine aussagenlogische Formel F$F$
  • ist F$F$ erfüllbar?
• 3KNF-SAT (NP-Vollständigkeit gilt auch für n \geq 3$n \geq 3$)
  • gegeben eine aussagenlogische Formel F$F$ in 3KNF
  • ist F$F$ erfüllbar?
• KNF-SAT
  • gegeben eine aussagenlogische Formel F$F$ in KNF
  • ist F$F$ erfüllbar?
• HAMILTON = \{G \; | \; G \text{ hat Hamiltonkreis}\}$= \{G \; | \; G \text{ hat Hamiltonkreis}\}$
  • gegeben ein Graph G$G$
  • hat G$G$ einen Hamiltonkreis?
• RUCKSACK = \{\text{bin}(a_1)\#...\#\text{bin}(a_n)\#\text{bin}(c) \; | \; \exists R \subseteq \{1,...,n\} : \sum_{i \in R} a_i = c\}$= \{\text{bin}(a_1)\#...\#\text{bin}(a_n)\#\text{bin}(c) \; | \; \exists R \subseteq \{1,...,n\} : \sum_{i \in R} a_i = c\}$ (auch Teilsummenproblem benannt)
  • gegeben eine Menge von Gewichte, und eine Gewichtsschranke
  • gibt es eine Teilmenge, deren Gesamtgewicht gleich der Gewichtsschranke ist? (oder kleiner gleich)
• 3COL (auch allgemein COL mit zusätzliche Zahl k$k$)
  • gegeben ein ungerichteter Graph
  • gibt es eine Färbung der Knoten mit 3 Farben, so dass keine benachbarten Knoten gleich gefärbt sind?
• SET-COVER / MENGENÜBERDECKUNG
  • gegeben eine Menge M$M$, Liste von Teilmengen von M$M$ und eine Zahl k$k$
  • kann man k$k$ von den Teilmengen wählen, die M$M$ überdecken?
• CLIQUE
  • gegeben ein Graph G$G$ und eine Zahl k$k$
  • hat G$G$ eine Clique der Größe k$k$?
• PARTITION
  • gegeben Zahlen a_1,...a_n \in \N$a_1,...a_n \in \N$
  • kann man die Zahlen in zwei Mengen S_1$S_1$ und \overline S_1$\overline S_1$ aufteilen, so dass die Summe der Zahlen in S_1$S_1$ gleich der Summe der Zahlen in \overline S_1$\overline S_1$ ist?
• BIN PACKING
  • gegeben eine Anzahl k$k$ von Behältern der Größe b$b$ und eine Anzahl n$n$ Objekte mit den Größen a_1,...a_n \leq b$a_1,...a_n \leq b$
  • können die n$n$ Objekte so auf die k$k$ Behälter verteilt werden, dass keiner der Behälter überläuft?
    • formal: \exists f: \{1,...,n\} \to \{1,...,k\} \forall j \in \{1,...,k\} : \sum_{f(i)=j}a_i \leq b$\exists f: \{1,...,n\} \to \{1,...,k\} \forall j \in \{1,...,k\} : \sum_{f(i)=j}a_i \leq b$?
• TRAVELING SALESMAN PROBLEM (TSP)
  • gegeben eine Entfernungsmatrix M_{ij} \in \N^{n \times n}$M_{ij} \in \N^{n \times n}$ und eine Zahl k \in \N$k \in \N$
  • gibt es einen Hamiltonkreis der Länge \leq k$\leq k$?

Aussagenlogik

• Aussagenlogik: bestehend aus Formeln und Variablen
  • Formeln: F \to \neg F \;|\; (F \land F) \;|\; (F \lor F) \;|\; X$F \to \neg F \;|\; (F \land F) \;|\; (F \lor F) \;|\; X$ (siehe DS für synt. Zucker...)
  • Variablen: X \to x \;|\; y \;|\; z \;|\; ...$X \to x \;|\; y \;|\; z \;|\; ...$
  • Belegung: Funktion \sigma$\sigma$ von Variablen auf \{0,1\}$\{0,1\}$
  • Erfüllbarkeit: F$F$ erfüllbar \iff \exists \sigma: \sigma(F) = 1$\iff \exists \sigma: \sigma(F) = 1$ (es gibt eine Belegung von Variablen in der Wahrheitstabelle, so dass für die Formel "wahr" steht)
  • Unerfüllbarkeit: F$F$ unerfüllbar \iff \forall \sigma: \sigma(F) = 0$\iff \forall \sigma: \sigma(F) = 0$ (es gibt keine Belegung von Variablen in der Wahrheitstabelle, so dass für die Formel "wahr" steht)
  • Tautologie / Allgemeingültigkeit / Gültigkeit: F$F$ allgemeingültig / gültig \iff \forall \sigma: \sigma(F) = 1$\iff \forall \sigma: \sigma(F) = 1$ (für jede Belegung von Variablen ist die Formel wahr)
  • (!) F_1 \leftrightarrow F_2$F_1 \leftrightarrow F_2$ (äquivalent) \iff (F_1 \land \neg F_2) \lor (\neg F_1 \land F_2)$\iff (F_1 \land \neg F_2) \lor (\neg F_1 \land F_2)$ nicht erfüllbar
  • (!) F$F$ erfüllbar \implies \overline F$\implies \overline F$ ungültig
  • (!) F$F$ unerfüllbar \implies \overline F$\implies \overline F$ gültig
• Konjunktive Normalform (KNF): Konjunktion von Klauseln (K_1 \land ... \land K_n$K_1 \land ... \land K_n$)
  • Klausel: Disjunktion von Literalen
  • Literal: Variable oder negierte Variable
  • n$n$KNF: KNF, wobei jede Klausel höchstens n$n$ Literale hat